Question

Show that the axes are to be rotated through an angle of $\dfrac{1}{2}{{\tan }^{-1}}\left( \dfrac{2h}{a-b} \right)$ so as to remove the $xy$ term from the equation $a{{x}^{2}}+2hxy+b{{y}^{2}}=0$, if $a\ne b$ & through an angle $\dfrac{\pi }{4}$, if $a=b$?

Answer 1

Hint: We start solving the problem by assuming that the axes is rotated through an angle $\theta $ in order to get $x'y'$ axes. We know that if axes are rotated through an angle $\theta $, then the old coordinates are $x=x'\cos \theta -y'\sin \theta $ and $y=x'\sin \theta +y'\cos \theta $. We substitute this in the given equation of the pair of lines and equate the coefficient of $x'y'$ term to zero. We then make the necessary calculations to get the value of $\theta $. After finding the value of $\theta $, we replace ‘b’ with ‘a’ in it to get the value of angle if $a=b$.

Complete step-by-step answer:
According to the problem, we need to prove that the axes are to be rotated through an angle of $\dfrac{1}{2}{{\tan }^{-1}}\left( \dfrac{2h}{a-b} \right)$ so as to remove the $xy$ term from the equation $a{{x}^{2}}+2hxy+b{{y}^{2}}=0$, if $a\ne b$ & through an angle $\dfrac{\pi }{4}$, if $a=b$.
Let us assume that the axes are to be rotated at an angle $\theta $ and $x'y'$ be new axes.

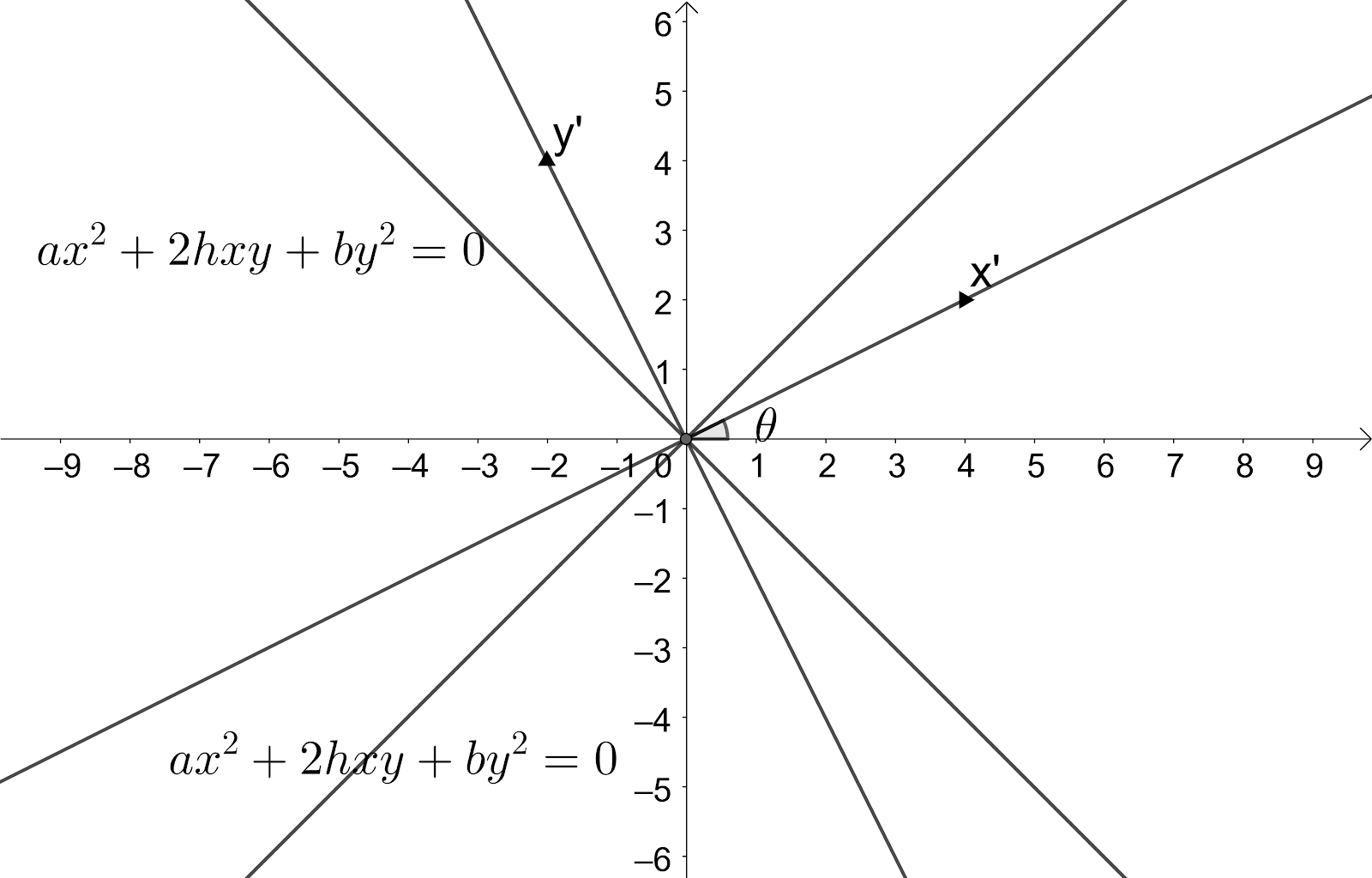
So, we know that the values of the old coordinates are $x=x'\cos \theta -y'\sin \theta $ and $y=x'\sin \theta +y'\cos \theta $. Let us substitute these results in the given equation of the pair of lines $a{{x}^{2}}+2hxy+b{{y}^{2}}=0$.
So, we get $a{{\left( x'\cos \theta -y'\sin \theta \right)}^{2}}+2h\left( x'\cos \theta -y'\sin \theta \right)\left( x'\sin \theta +y'\cos \theta \right)+b{{\left( x'\sin \theta +y'\cos \theta \right)}^{2}}=0$.
We need to remove $xy$ term from this equation, which means that the coefficient of $xy$ term is 0. Let us find the coefficient of $xy$ term from the above equation.
So, we get the coefficient as $-2a\sin \theta \cos \theta +2h{{\cos }^{2}}\theta -2h{{\sin }^{2}}\theta +2b\sin \theta \cos \theta $ and this should be equal to zero.
So, we have $-2a\sin \theta \cos \theta +2h{{\cos }^{2}}\theta -2h{{\sin }^{2}}\theta +2b\sin \theta \cos \theta =0$.
$\Rightarrow 2\sin \theta \cos \theta \left( b-a \right)+2h\left( {{\cos }^{2}}\theta -{{\sin }^{2}}\theta \right)=0$.
We know that $\sin 2\theta =2\sin \theta \cos \theta $ and \[{{\cos }^{2}}\theta -{{\sin }^{2}}\theta =\cos 2\theta \].
$\Rightarrow \left( b-a \right)\sin 2\theta +2h\cos 2\theta =0$.
$\Rightarrow \left( a-b \right)\sin 2\theta =2h\cos 2\theta $.
$\Rightarrow \dfrac{\sin 2\theta }{\cos 2\theta }=\dfrac{2h}{a-b}$.
$\Rightarrow \tan 2\theta =\dfrac{2h}{a-b}$.
$\Rightarrow 2\theta ={{\tan }^{-1}}\left( \dfrac{2h}{a-b} \right)$.
$\Rightarrow \theta =\dfrac{1}{2}{{\tan }^{-1}}\left( \dfrac{2h}{a-b} \right)$ ---(1).
So, we have found that the axes have to be rotated through $\theta =\dfrac{1}{2}{{\tan }^{-1}}\left( \dfrac{2h}{a-b} \right)$ if $a\ne b$.
Let us assume $a=b$ and we substitute this in equation (1).
So, we have $\theta =\dfrac{1}{2}{{\tan }^{-1}}\left( \dfrac{2h}{a-a} \right)$.
$\Rightarrow \theta =\dfrac{1}{2}{{\tan }^{-1}}\left( \dfrac{2h}{0} \right)$.
$\Rightarrow \theta =\dfrac{1}{2}{{\tan }^{-1}}\left( \infty \right)$.
$\Rightarrow \theta =\dfrac{1}{2}\times \dfrac{\pi }{2}$.
$\Rightarrow \theta =\dfrac{\pi }{4}$.
So, we have found that the axes have to be rotated through $\theta =\dfrac{\pi }{4}$ if $a=b$.

Note: We can see that the problem contains a good amount of calculation, so we need to perform each step carefully. We should not confuse the shifting of axes and rotation of axes while solving this problem. We can also solve this problem by assuming the values in place of variables ‘a’, ‘b’ and ‘h’. Similarly, we can expect to find the angle if the axes are shifted instead of rotation.