Question

Show that the angles of an equilateral triangle are \[{60^\circ}\] each.

Answer 1

Hint: We have given an equilateral triangle. So, we know that all three sides of this triangle are equal. By using this information we will prove that all three angles are also equal. After that we will prove, the angles of an equilateral triangle are \[{60^\circ}\] each by using the angle sum property of the triangle.
Angle sum property of a triangle states that the sum of interior angles of a triangle is ${180^\circ}$.

Complete step-by-step solution:
For better understanding, we will draw a diagram of a triangle.

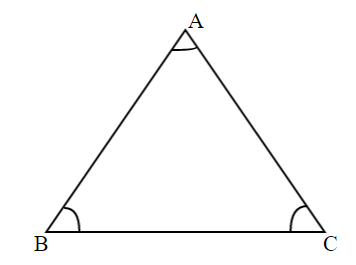
Here we have to prove that,
$\angle A = \angle B = \angle C = {60^\circ}$
We have given,
AB = AC
So, by the property, the angles opposite to equal sides are equal.
$ \Rightarrow \angle B = \angle C$ ………….1)
Also, we have,
AC = BC
Similarly as above,
$ \Rightarrow \angle B = \angle A$ ………….. 2)
From 1) & 2)
We have,
$\angle A = \angle B = \angle C$ …………… 3)
Now, we know the angle sum property of a triangle is the sum of all interior angles is ${180^\circ}$.
In $\vartriangle ABC$,
$\angle A + \angle B + \angle C = {180^\circ}$
From 3)
$ \Rightarrow \angle A = \angle A = \angle A = {180^\circ}$
So, we can say that,
$ \Rightarrow 3\angle A = {180^\circ}$
To find the measure of $\angle A$, we have to divide by 3 into both sides.
\[ \Rightarrow \angle A = \dfrac{{{{180}^\circ}}}{3}\]
Simplify it.
$ \Rightarrow \angle A = {60^\circ}$
From 3)
$\therefore \angle A = \angle B = \angle C = {60^\circ}$

Hence we proved that angles of an equilateral triangle are ${60^\circ}$ each.

Note: Applications of an equilateral triangle.
1) Surveying: In surveying, the equilateral triangle method (34) is used to measure around obstacles.
2) Satellite geodesy: In satellite geodesy, an equilateral triangle on the earth with sides roughly 900 limes long was first used in 1962 to verify the accuracy of the satellite triangulation concept.
3) GPS antenna: An equilateral triangular receiving antenna can be used in the global positioning system (GPS).
4) Lisa and gravitational waves: Launching in 2020 at the earliest, LISA (Laser Interferometer Space Antenna) will overtake the large hadrons.