Question

Show that of all line segments drawn from a point to a line which is not on it, the perpendicular distance is the shortest distance.

Answer 1

Hint: We solve this problem by using the negation of a statement. First we assume that the perpendicular distance is not the shortest distance and we assume that some other system as a shortest distance. Then we use the Pythagoras theorem to prove that our assumption is wrong.
The Pythagoras Theorem states that the square of hypotenuse is equal to sum of squares of other two sides that is for the triangle shown below

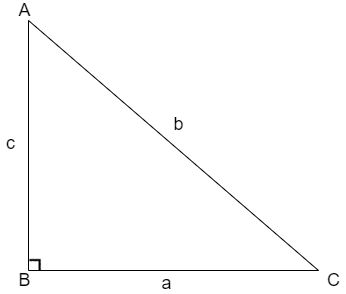
The Pythagoras theorem is given as \[{{b}^{2}}={{a}^{2}}+{{c}^{2}}\].

Complete step by step answer:
We are asked to prove that of all line segments drawn from the given point to a line which is not on the line, the perpendicular distance is the shortest.
Let us draw a figure that represents the given condition then we get

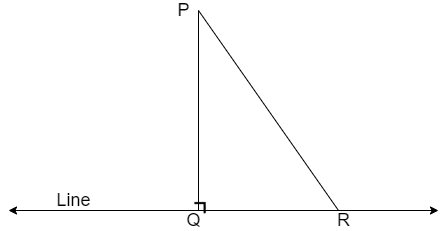
Here, we can see that the line segment PQ is perpendicular distance to line.
Now, let us assume that the PQ is not the shortest distance from the given point P to line.
So, let us consider a random line segment from P to line marked as PR.
We know that the Pythagoras Theorem states that the square of hypotenuse is equal to sum of squares of other two sides that is for the triangle shown below

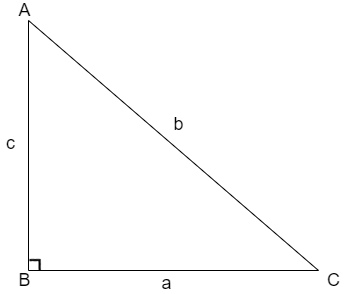
The Pythagoras theorem is given as \[{{b}^{2}}={{a}^{2}}+{{c}^{2}}\].
Now, let us consider the triangle \[\Delta PQR\]
Now, by applying the Pythagoras theorem we get
\[\Rightarrow P{{R}^{2}}=P{{Q}^{2}}+Q{{R}^{2}}\]
Here we can see that we need to add some value to \[P{{Q}^{2}}\] so as to get \[P{{R}^{2}}\]
So, by converting the above equation into inequalities we get
\[\Rightarrow P{{R}^{2}} > P{{Q}^{2}}\]
Now, by applying the square root on both sides we get
\[\Rightarrow PR > PQ\]
Here we can see that PR is greater than PQ.
But our assumption says that PR is the shortest among all line segments which is not a perpendicular distance.
So, we can say that our assumption of taking the perpendicular distance is not the shortest distance is wrong.
Therefore, we can say that the perpendicular distance is the shortest.
Hence the required result has been proved.

Note: We can solve this problem by using the other method.
Now, let us assume that the PQ is not the shortest distance from the given point P to line.
So, let us consider a random line segment from P to line marked as PR.

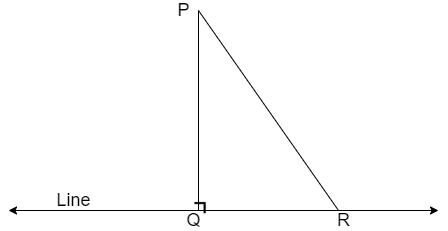
Let us consider the triangle \[\Delta PQR\]
We know that the sum of angles of a triangle equals to \[{{180}^{\circ }}\] then we get
\[\Rightarrow \angle P+\angle Q+\angle R={{180}^{\circ }}\]
We know that \[\angle Q={{90}^{\circ }}\] then we get
\[\Rightarrow \angle P+\angle R={{90}^{\circ }}\]
Here, we can see that we need to add some angle to \[\angle R\] so as to get \[{{90}^{\circ }}\]
So, by using the inequalities we get
\[\begin{align}
  & \Rightarrow \angle R < {{90}^{\circ }} \\
 & \Rightarrow \angle R < \angle Q \\
\end{align}\]
We know that the side opposite to greater angle is longer than the side opposite to smaller angle
By using the above condition we get
\[\Rightarrow PR > PQ\]
Here we can see that PR is greater than PQ.
But our assumption says that PR is the shortest among all line segments which is not a perpendicular distance.
So, we can say that our assumption of taking the perpendicular distance is not the shortest distance is wrong.
Therefore, we can say that the perpendicular distance is the shortest.
Hence the required result has been proved.