Question

Show that in a right-angled triangle, the hypotenuse is the longest side.

Answer 1

Hint: The side opposite to greater angles is always longer in a triangle. A triangle is a polygon with three edges and three vertices, which are the basic shapes in geometry. It is a closed two-dimensional shape with three straight sides.
Here, in this question, we need to prove that the hypotenuse of the right-angled triangle is the longest side of the triangle. For this, we need to follow the properties of the triangles. One of the properties of the triangle that is used in solving the question is that the side opposite to the greater angle is longer.

Complete step-by-step answer:
Given the triangle is a right-angled triangle, which means one of the angles of the triangle is \[{90^ \circ }\]

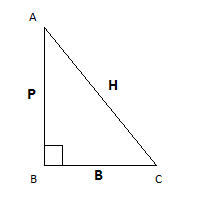
In triangle ABC\[\angle B = {90^ \circ }\], where AC is hypotenuse, BC is the base, and AB is the perpendicular
By using the Angle sum property of the triangle we can write
\[\angle A + \angle B + \angle C = {180^ \circ }\]
\[\angle A + {90^ \circ } + \angle C = {180^ \circ }\] [Since\[\angle B = {90^ \circ }\]]
\[
  \angle A + \angle C = {180^ \circ } - {90^ \circ } \\
   = {90^ \circ } \\
 \]
Hence we can say
\[\angle A < \angle B\]
\[\angle C < \angle B\]
Since \[\angle A + \angle C = {90^ \circ }\]
Now by using the property Side opposite to the greater angle is longer, we can say
\[AB < AC\]
\[BC < AC\]
Therefore, side AC which is the hypotenuse of\[\vartriangle ABC\]is the longest side of the right triangle.
Hence Proved

Note: Students must remember one of the properties of the triangle that the side opposite to the greater angle is longer and the vice versa is also true. A triangle has three sides, and their type depends on the length of its sides and the size of its angles. There are basically three types of triangles based on the measurement of the angles, namely: Acute Triangle, Obtuse Triangle, and Right Triangle.
An acute triangle is a triangle with three acute angles, and the obtuse triangles are the triangle with one obtuse angle where the acute angle is an angle less than \[{90^ \circ }\]an obtuse angle is an angle more than\[{90^ \circ }\]. But when one of the angles of the triangle becomes \[{90^ \circ }\], then the triangle is known as a Right-angled triangle.