Question

Show‌ ‌that‌ ‌in‌ ‌a‌ ‌quadrilateral‌ ‌ABCD,‌ ‌ ‌
$AB+BC+CD+DA<2\left(‌ ‌BD+AC‌ ‌\right)$‌

Answer 1

Hint: We solve this problem by using the basic principle of triangle that is the sum of any two sides is greater than the third side. Suppose there is a triangle $\Delta ABC$ as shown below then the basic principle states that,

$AB+BC > AC$ and $AB+AC > BC$ and $BC+AC > AB$
By using this property in all possible triangles that are formed in a quadrilateral we can prove the required result.

Complete step-by-step solution:
Let us take some random quadrilateral ABCD and join the opposite vertices as shown below.

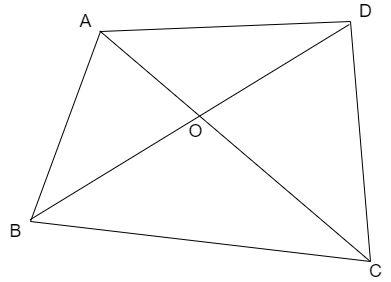
Now, let us use the basic triangle property for all triangles possible in the above quadrilateral.
We know that the basic property of $\Delta ABC$ is given as that sum of any two sides should be greater than third side that is,

$AB+BC > AC$ and $AB+AC > BC$ and $BC+AC > AB$
Now, let us assume the triangle $\Delta AOB$ from the quadrilateral ABCD and applying the above property then we get,
$\Rightarrow AO+BO > AB............(i)$
Now, let us assume the triangle $\Delta BOC$ from the quadrilateral ABCD and applying the above property then we get,
$\Rightarrow CO+BO > BC............(ii)$
Now, let us assume the triangle $\Delta COD$ from the quadrilateral ABCD and applying the above property then we get,
$\Rightarrow CO+DO > DC............(iii)$
Now, let us assume the triangle $\Delta DOA$ from the quadrilateral ABCD and applying the above property then we get,
$\Rightarrow AO+DO > DA............(iv)$
Now, let us add all the four equations that we got from four different triangles then we get,
$\begin{align}
  & \Rightarrow \left( AO+BO \right)+\left( CO+BO \right)+\left( CO+DO \right)+\left( AO+DO \right) > AB+BC+CD+DA \\
 & \Rightarrow 2\left( AO+BO+CO+DO \right) > AB+BC+CD+DA \\
\end{align}$
Now, let us rearrange the terms inside the brackets of LHS as,
$\Rightarrow 2\left( \left( AO+DO \right)+\left( BO+CO \right) \right) > AB+BC+CD+DA$
Here, we can see that the diagonals in the quadrilateral ABCD can be written as,
$\begin{align}
  & \Rightarrow AD=AO+DO \\
 & \Rightarrow BC=BO+CO \\
\end{align}$
By using these equations in above inequality then we get,
$\begin{align}
  & \Rightarrow 2\left( AD+BC \right) > AB+BC+CD+DA \\
 & \Rightarrow AB+BC+CD+DA<2\left( AD+BC \right) \\
\end{align}$
Hence the required result has been proved.

Note: The main mistake that is done in taking the quadrilateral. We are given that the quadrilateral is ABCD in which the vertices should be named in that order only then we get the figure as,

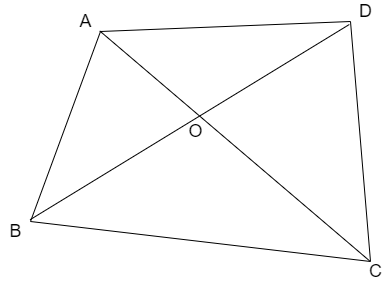
But some students may rearrange the vertices and may take the quadrilateral as,

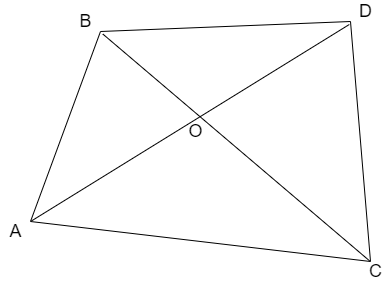
This is very wrong because the representation of quadrilaterals or triangles or any other polygons should be done in the same order as the naming.