Question

Show that if the diagonals of the quadrilateral are equal and bisect each other at right angles, then it is a square.

Answer 1

Hint: Here, first we have to prove that the quadrilateral ABCD is a parallelogram by the congruence of triangles. Then we will get all sides of ABCD are equal. Next, we have to show that all angles are equal again by the congruence of triangles. Now, to prove each angle is ${{90}^{\circ }}$ we have to consider the transversal BC and apply the property of transversal that interior angles on the same side of the transversal are supplementary.

Complete step-by-step answer:
First let us draw the figure.

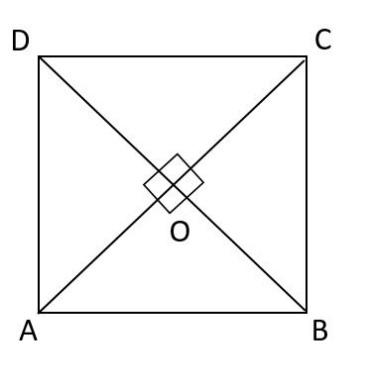
Here, we are given that the diagonals of the quadrilateral ABCD are equal and bisect each other at ${{90}^{\circ }}$.
 Next, we have to prove that the quadrilateral ABCD is a square.
A square is a quadrilateral having all four sides equal and each angle is ${{90}^{\circ }}$. So, here first we have to prove that ABCD is a parallelogram and all four sides are equal.
Since, it is given the diagonals of ABCD are equal, we can write:
AC = BD
The diagonals also bisect each other at ${{90}^{\circ }}$ so, we can say that:
$\begin{align}
  & \begin{array}{*{35}{l}}
   OA\text{ }=\text{ }OC~ \\
   OB\text{ }=\text{ }OD \\
\end{array} \\
 & \angle AOB=\angle BOC=\angle COD=\angle AOD={{90}^{\circ }} \\
\end{align}$
 Consider two triangles $\Delta AOB$ and $\Delta COB$,
$\begin{align}
  & OA=OC \\
 & \angle AOB=\angle BOC={{90}^{\circ }} \\
\end{align}$
We also have a common side OB.
Therefore, by SAS congruence rule we can say that:
$\Delta AOB\cong \Delta COB$
Hence, if two triangles are congruent, we can say that all the corresponding sides and angles are equal.
Therefore, we will get:
$AB=BC$ ….. (1)
Now, consider the triangles $\Delta BOC$ and $\Delta COD$,
We have:
$\begin{align}
  & BO=OD \\
 & \angle BOC=\angle COD={{90}^{\circ }} \\
\end{align}$
Also, we have the common side OC.
Therefore, by SAS congruence rule we can say that:
$\Delta BOC\cong \Delta COD$
Hence, by the corresponding part of congruence triangles we will get:
$BC=CD$ ….. (2)
Next, consider the triangles $\Delta COD$ and $\Delta AOD$, we will obtain:
$\begin{align}
  & OA=OC \\
 & \angle AOD=\angle COD \\
\end{align}$
Also the common side is OD.
Therefore, by the SAS congruence rule we can say that:
$\Delta COD\cong \Delta AOD$
 Hence, by the corresponding part of congruence triangles we will get:
$CD=AD$ ….. (3)
Hence, by the equation (1), equation (2) and equation (3) we can say that:
$AB=BC=CD=AD$
Therefore, we can say that all the sides of ABCD are equal and hence, it is a parallelogram.
Now, we have to prove that all angles of ABCD are equal.
For that consider the triangles $\Delta ABC$ and $\Delta DCB$ we will obtain:
$AC=BD$, since the diagonals of ABCD are equal.
We know that the opposite sides of a parallelogram are equal, we will get:
$AB=CD$
We have the common side BC.
Here, we have got that three sides are equal. Hence, by SSS congruence rule, we will get:
$\Delta ABC\cong \Delta DCB$
Hence, by corresponding parts of congruence triangles we will obtain:
$\angle B=\angle C$ ….. (4)
Now, consider the triangles $\Delta DCB$ and $\Delta ADC$. We will get:
$AD=BC$, as they are the opposite sides of a parallelogram.
Since, the diagonals are equal, we will get:
$AC=BD$
We have the common side CD.
Therefore, by SSS congruence rule, we will get:
$\Delta DCB\cong \Delta ADC$
Hence, by corresponding part of congruence triangles, we will obtain:
$\angle C=\angle D$ ….. (5)
Now, consider the triangles $\Delta ADC$ and $\Delta BAD$ we will get:
$AB=CD$, as the opposite sides of parallelogram are equal.
$AC=BD$, since the diagonals are equal.
We have the common side AD.
Therefore, by SSS congruence rule, we will get:
$\Delta ADC\cong \Delta BAD$
Hence, by the corresponding part of congruence triangles, we will obtain:
$\angle A=\angle D$ ….. (6)
Therefore from equation (4), equation (5) and equation (6) we can say that:
$\angle A=\angle B=\angle C=\angle D$ …. (7)
Next, we have to prove that all the angles of ABCD are ${{90}^{\circ }}$.
Now, we have $AB\parallel CD$, since opposite sides of the parallelogram are parallel and BC is the transversal.
Hence, by the property of transversal we know that the interior angles on the same side of the transversal are supplementary, that is sum is ${{180}^{\circ }}$. Therefore, we can write:
$\angle B+\angle C={{180}^{\circ }}$
We know that $\angle B=\angle C$, we will get:
$\begin{align}
  & \angle B+\angle B={{180}^{\circ }} \\
 & 2\angle B={{180}^{\circ }} \\
\end{align}$
By, cross multiplication we will obtain:
$\angle B=\dfrac{{{180}^{\circ }}}{2}$
Hence, by cancellation we get:
$\angle B={{90}^{\circ }}$
Therefore, by equation (7) we can say that:
$\angle A=\angle B=\angle C=\angle D={{90}^{\circ }}$
Here, we got that all the sides are equal and all the four angles are ${{90}^{\circ }}$.
Therefore, we can say that the parallelogram ABCD is a square.

Note: Here, to prove that ABCD is a square first you have to prove that it is a parallelogram since, every square is a parallelogram. And to show that every angle is ${{90}^{\circ }}$, you can also apply the property that the sum of the angles of a quadrilateral is ${{360}^{\circ }}$.