
How do you show that $f(x) = 2x\;{\text{and}}\;g(x) = \dfrac{x}{2}$ are inverse functions algebraically and graphically?
Answer
543.6k+ views
Hint: To proof algebraically use composite function and show output of $fog(x) = gof(x)$ equals input that is $x$. And to proof it graphically, plot graphs of both the lines and show that they are symmetric about the line $x = y$
Complete step by step solution:
Proving that $f(x) = 2x\;{\text{and}}\;g(x) = \dfrac{x}{2}$ are inverse functions algebraically:
To show $f(x) = 2x\;{\text{and}}\;g(x) = \dfrac{x}{2}$ are inverse function algebraically, we will first find the composite function $fog(x)\;{\text{and}}\;gof(x)$
Composite function $fog(x)$ will be written in the way that we will take function $g(x)$ as the argument of the function $f(x)$ as follows
\[
f(g(x)) = 2\left( {g(x)} \right) \\
= 2 \times \dfrac{x}{2} \\
= x \\
\]
Now similarly finding $gof(x)$, we will get
$
gof(x) = \dfrac{{f(x)}}{2} \\
= \dfrac{{2x}}{2} \\
= x \\
$
So we can see that the composite functions are giving the output equals input that is $fog(x) = gof(x) = x$
Therefore we can say that $f(x)\;{\text{and}}\;g(x)$ are inverse functions.
Again proving their inverse nature towards each other graphically,
We will plot the graph of $f(x) = 2x\;{\text{and}}\;g(x) = \dfrac{x}{2}$ and then see if they will be symmetric about the line $x = y$ or not. And if they will be symmetric then they are inverse function to each other.
Now to plot the graph we will rewrite the equations as
$y = 2x\;{\text{and}}\;y = \dfrac{x}{2}$
We will first find some points of both the equations, to plot their graph, so collecting points as follows
So we get $\left( {0,\;0} \right)\;{\text{and}}\;\left( {2,\;4} \right)$ as points of graph for first equation and $\left( {0,\;0} \right)\;{\text{and}}\;\left( {2,\;1} \right)$ as points of graph for second equation. So plotting their graph:
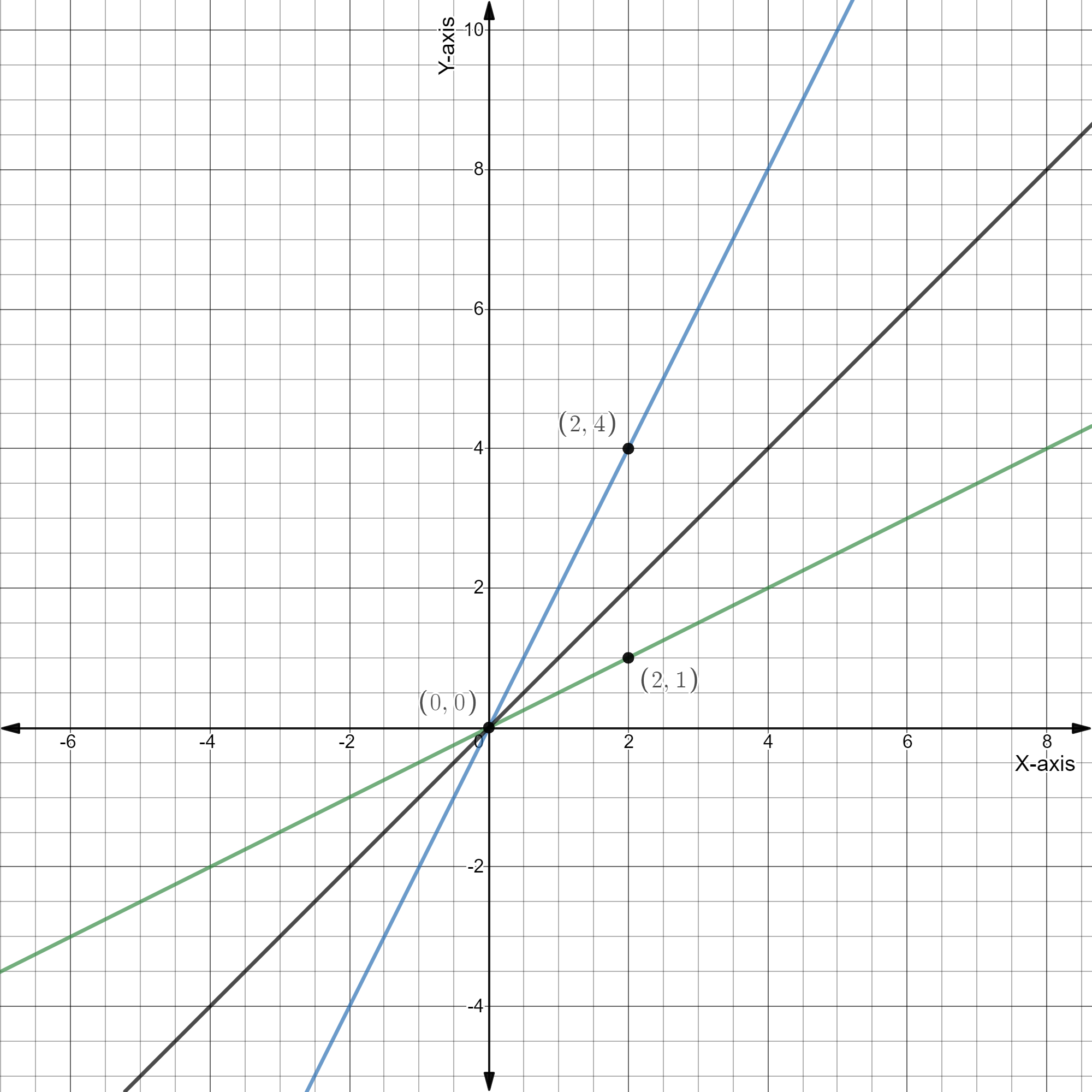
Blue line represents $f(x) = 2x$
Green line represents $g(x) = \dfrac{x}{2}$
And black line represents $x = y$
So we can clearly see that the green and blue lines are symmetric about black line. Hence proved
Note: Find such points to graph the equations that are firstly should be at reasonable distance from each other and also should have the whole number value (so that you can plot them easily). Also take the scale of the graph according to the points.
Complete step by step solution:
Proving that $f(x) = 2x\;{\text{and}}\;g(x) = \dfrac{x}{2}$ are inverse functions algebraically:
To show $f(x) = 2x\;{\text{and}}\;g(x) = \dfrac{x}{2}$ are inverse function algebraically, we will first find the composite function $fog(x)\;{\text{and}}\;gof(x)$
Composite function $fog(x)$ will be written in the way that we will take function $g(x)$ as the argument of the function $f(x)$ as follows
\[
f(g(x)) = 2\left( {g(x)} \right) \\
= 2 \times \dfrac{x}{2} \\
= x \\
\]
Now similarly finding $gof(x)$, we will get
$
gof(x) = \dfrac{{f(x)}}{2} \\
= \dfrac{{2x}}{2} \\
= x \\
$
So we can see that the composite functions are giving the output equals input that is $fog(x) = gof(x) = x$
Therefore we can say that $f(x)\;{\text{and}}\;g(x)$ are inverse functions.
Again proving their inverse nature towards each other graphically,
We will plot the graph of $f(x) = 2x\;{\text{and}}\;g(x) = \dfrac{x}{2}$ and then see if they will be symmetric about the line $x = y$ or not. And if they will be symmetric then they are inverse function to each other.
Now to plot the graph we will rewrite the equations as
$y = 2x\;{\text{and}}\;y = \dfrac{x}{2}$
We will first find some points of both the equations, to plot their graph, so collecting points as follows
| $x$ | $y = 2x$ | $y = \dfrac{x}{2}$ | Coordinates for graph of first equation | Coordinates for graph of second equation |
| $0$ | $0$ | $0$ | $\left( {0,\;0} \right)$ | $\left( {0,\;0} \right)$ |
| $2$ | $4$ | $1$ | $\left( {2,\;4} \right)$ | $\left( {2,\;1} \right)$ |
So we get $\left( {0,\;0} \right)\;{\text{and}}\;\left( {2,\;4} \right)$ as points of graph for first equation and $\left( {0,\;0} \right)\;{\text{and}}\;\left( {2,\;1} \right)$ as points of graph for second equation. So plotting their graph:

Blue line represents $f(x) = 2x$
Green line represents $g(x) = \dfrac{x}{2}$
And black line represents $x = y$
So we can clearly see that the green and blue lines are symmetric about black line. Hence proved
Note: Find such points to graph the equations that are firstly should be at reasonable distance from each other and also should have the whole number value (so that you can plot them easily). Also take the scale of the graph according to the points.
Recently Updated Pages
Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE

RNA and DNA are chiral molecules their chirality is class 12 chemistry CBSE




