Question

Show that $\cos {{32}^{\circ }}\cos {{58}^{\circ }}-\sin {{32}^{\circ }}\sin {{58}^{\circ }}=0$ \[\]

Answer 1

Hint: We recall the definitions of sine and cosine trigonometric ratios. We use the relation of complementary angles between sine and cosine $\sin \theta =\cos \left( {{90}^{\circ }}-\theta \right)$ and $\cos \theta =\sin \left( {{90}^{\circ }}-\theta \right)$ (also known as reduction formula) to convert cosine into sine or to convert sine into cosine to prove the given statement.\[\]

Complete step by step answer:

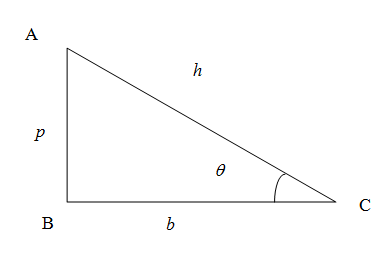
We know that in right angled triangle (Here ABC) the side opposite to right angle(Here $\angle B$) is called hypotenuse denoted as $AC=h$, the vertical side is called perpendicular denoted as $AB=p$ and the horizontal side is called the base denoted as $BC=b$.\[\]
We know from the trigonometric ratios in a right angled triangle the sine of any angle is given by the ratio of side opposite to the angle to the hypotenuse. In the figure the sine of the angle $\angle C=\theta $ is given by
\[\sin \theta =\dfrac{p}{h}\]
Similarly the cosine of an angle is the ratio of side adjacent to the angle (excluding hypotenuse) to the hypotenuse. So we have cosine of angle $\theta $
\[\cos \theta =\dfrac{b}{h}\]
We know that the sum of angles in a triangle is ${{180}^{\circ }}$. So we have in triangle ABC
\[\begin{align}
  & \angle A+\angle B+\angle C={{180}^{\circ }} \\
 & \Rightarrow \angle A+\angle C={{90}^{\circ }}\left( \because \angle B={{90}^{\circ }} \right) \\
 & \Rightarrow \angle A={{90}^{\circ }}-\angle C={{90}^{\circ }}-\theta \\
\end{align}\]
Let see the sine and cosines of angles $\angle A,\angle C$ .We have,
\[\begin{align}
  & \sin C=\sin \theta =\dfrac{p}{h},\cos C=\cos \theta =\dfrac{b}{h} \\
 & \sin A=\sin \left( {{90}^{\circ }}-\theta \right)=\dfrac{b}{h},\cos A=\cos \left( {{90}^{\circ }}-\theta \right)=\dfrac{p}{h} \\
\end{align}\]
So we have,
\[\begin{align}
  & \cos \left( {{90}^{\circ }}-\theta \right)=\sin \theta \\
 & \sin \left( {{90}^{\circ }}-\theta \right)=\cos \theta \\
\end{align}\]
The above identity is true for all acute angles $\theta $ and is called reduction formula of sine and cosine or reflection identity about $\dfrac{\pi }{4}$ because the complementary angles $\theta ,{{90}^{\circ }}-\theta $ reflect each other about the angle $\dfrac{\pi }{4}$. We are given in the question the following statement to prove,
\[\cos {{32}^{\circ }}\cos {{58}^{\circ }}-\sin {{32}^{\circ }}\sin {{58}^{\circ }}=0\]
We see the trigonometric expressions in sine and cosine has angles $\theta ={{32}^{\circ }},{{58}^{\circ }}$. We add both the angles to find ${{32}^{\circ }}+{{58}^{\circ }}={{90}^{\circ }}$. So they are complementary angles. We use the reduction formula of sine and cosine taking $\theta ={{32}^{\circ }}$ to have,
\[\begin{align}
  & \cos {{58}^{\circ }}=\cos \left( {{90}^{\circ }}-{{32}^{\circ }} \right)=\sin {{32}^{\circ }} \\
 & \sin {{58}^{\circ }}=\sin \left( {{90}^{\circ }}-{{32}^{\circ }} \right)=\cos {{32}^{\circ }} \\
\end{align}\]
We use the above obtained values in the left hand side of statement to have,
\[\begin{align}
  & \cos {{32}^{\circ }}\cos {{58}^{\circ }}-\sin {{32}^{\circ }}\sin {{58}^{\circ }} \\
 & =\cos {{32}^{\circ }}\sin {{32}^{\circ }}-\sin {{32}^{\circ }}\cos {{32}^{\circ }}\left( \because \cos 58{}^{\circ }=\sin {{32}^{\circ }},\sin {{58}^{\circ }}=\cos {{32}^{\circ }} \right) \\
 & =0 \\
\end{align}\]
Hence the statement is proved. \[\]

Note: We note that we have taken the smaller angle ${{32}^{\circ }}$ as $\theta $. for the reduction formula. We can also solve by taking the larger angle ${{58}^{\circ }}$ as $\theta .$ We must be careful of the difference between reduction formulas and shift by ${{90}^{\circ }}$ formulas which is given by $\sin \left( \theta \pm {{90}^{\circ }} \right)=\pm \cos \theta $ and $\cos \left( \theta \pm {{90}^{\circ }} \right)=\mp \sin \theta $.