Question

Show that \[A( - 3,2)\], \[B( - 5, - 5)\], \[C(2, - 3)\] and \[D(4,4)\] are the vertices of a rhombus.

Answer 1

Hint: We will prove that given points are vertices of a rhombus using the distance formula. We will find the distance \[AB\], \[BC\], \[CD\] and \[DA\], if all these lengths are equal then the given points will form a rhombus if all the sides of a rhombus are equal.
Formula Used:
We will use the formula to find the distance between two given points \[({x_1},{y_1})\] and \[({x_2},{y_2})\]which is given by \[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \].

Complete step-by-step answer:
We have to show that given points \[A( - 3,2)\], \[B( - 5, - 5)\], \[C(2, - 3)\] and \[D(4,4)\] are the vertices of a rhombus.
Let the point \[A( - 3,2)\], \[B( - 5, - 5)\], \[C(2, - 3)\] and \[D(4,4)\] be the vertices of a quadrilateral \[ABCD\].
Let’s draw the diagram showing all the given points.

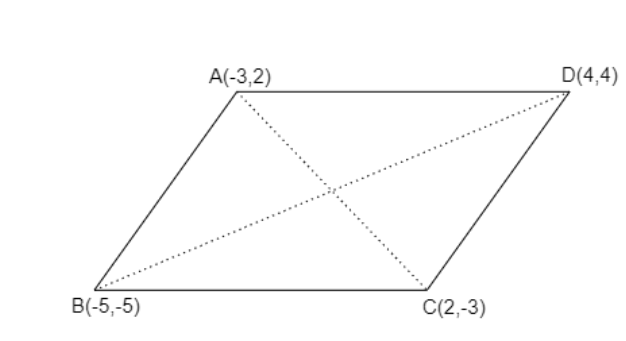
As we know that the length of all the sides of a rhombus is equal and the length of its diagonal are not equal.
We will find the length of each side to prove that points \[A( - 3,2)\], \[B( - 5, - 5)\], \[C(2, - 3)\] and \[D(4,4)\] are the vertices of a rhombus.
Now, we will find the distance \[AB\] using the distance formula.
We have \[A( - 3,2)\] and \[B( - 5, - 5)\].Therefore, using the distance formula we get
\[ \Rightarrow AB = \sqrt {{{\left( {\left( { - 5} \right) - ( - 3)} \right)}^2} + {{\left( {\left( { - 5} \right) - \left( 2 \right)} \right)}^2}} \]
Subtracting the terms in the bracket, we get
\[ \Rightarrow AB = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 7} \right)}^2}} \]
On solving,
\[ \Rightarrow AB = \sqrt {4 + 49} \]
On further simplification we get
\[ \Rightarrow AB = \sqrt {53} \]
Now, we will find the distance \[BC\] using the distance formula.
We have \[B( - 5, - 5)\] and \[C(2, - 3)\].Therefore, using the distance formula we get
\[ \Rightarrow BC = \sqrt {{{\left( {\left( 2 \right) - ( - 5)} \right)}^2} + {{\left( {\left( { - 3} \right) - \left( { - 5} \right)} \right)}^2}} \]
Subtracting the terms in the bracket, we get
\[ \Rightarrow BC = \sqrt {{{\left( 7 \right)}^2} + {{\left( 2 \right)}^2}} \]
On solving,
\[ \Rightarrow BC = \sqrt {49 + 4} \]
On further simplification we get
\[ \Rightarrow BC = \sqrt {53} \]
Now, we will find the distance \[CD\] using the distance formula.
We have \[C(2, - 3)\] and \[D(4,4)\].Therefore, using the distance formula we get
\[ \Rightarrow CD = \sqrt {{{\left( {\left( 4 \right) - (2)} \right)}^2} + {{\left( {\left( 4 \right) - \left( { - 3} \right)} \right)}^2}} \]
Subtracting the terms in the bracket, we get
\[ \Rightarrow CD = \sqrt {{{\left( 2 \right)}^2} + {{\left( 7 \right)}^2}} \]
On solving,
\[ \Rightarrow CD = \sqrt {4 + 49} \]
On further simplification we get
\[ \Rightarrow CD = \sqrt {53} \]
Now, we will find the distance \[DA\] using the distance formula.
We have \[D(4,4)\] and \[A( - 3,2)\].Therefore, using the distance formula we get
\[ \Rightarrow DA = \sqrt {{{\left( {\left( { - 3} \right) - (4)} \right)}^2} + {{\left( {\left( 2 \right) - \left( 4 \right)} \right)}^2}} \]
Subtracting the terms in the bracket, we get
\[ \Rightarrow DA = \sqrt {{{\left( { - 7} \right)}^2} + {{\left( { - 2} \right)}^2}} \]
On solving,
\[ \Rightarrow DA = \sqrt {49 + 4} \]
On further simplification we get
\[ \Rightarrow DA = \sqrt {53} \]
Also, we have length of diagonal \[AC\] as
\[ \Rightarrow AC = \sqrt {{{\left( {\left( 2 \right) - ( - 3)} \right)}^2} + {{\left( {\left( { - 3} \right) - \left( 2 \right)} \right)}^2}} \]
Subtracting the terms in the bracket, we get
\[ \Rightarrow AC = \sqrt {{{\left( 5 \right)}^2} + {{\left( { - 5} \right)}^2}} \]
On solving,
\[ \Rightarrow AC = \sqrt {25 + 25} \]
On further simplification we get
\[ \Rightarrow AC = \sqrt {50} \]
Now, we have length of diagonal \[BD\] as
\[ \Rightarrow BD = \sqrt {{{\left( {\left( 4 \right) - ( - 5)} \right)}^2} + {{\left( {\left( 4 \right) - \left( { - 5} \right)} \right)}^2}} \]
Subtracting the terms in the bracket, we get
\[ \Rightarrow BD = \sqrt {{{\left( 9 \right)}^2} + {{\left( 9 \right)}^2}} \]
On solving,
\[ \Rightarrow BD = \sqrt {81 + 81} \]
On further simplification we get
\[ \Rightarrow BD = \sqrt {162} \]
Therefore, we can see that \[AB = BC = CD = DA\] and \[AC \ne BD\] i.e., length of all the sides is equal and diagonals are not equal.
Hence, points \[A( - 3,2)\], \[B( - 5, - 5)\], \[C(2, - 3)\] and \[D(4,4)\] are the vertices of a rhombus.


Note: We can also prove that the given points are vertices of a rhombus by first finding the midpoint of both the diagonals \[AC\] and \[BD\] using the midpoint formula. If the midpoint of both the diagonals lies on the same point then it forms a parallelogram. Then we will find the length of opposite sides, if the length of opposite sides is equal then it is a rhombus.