Question

Show how you would connect three resistors each of resistance $6\Omega $. So that the combination has a resistance of $(i)9\Omega $ $(ii)4\Omega $.

Answer 1

Hint: We know that there are two possible combinations of resistors. One is the series combination and the other one is a parallel combination. A series combination of resistors is the same in all the resistors and the potential difference of the combination is the sum of the potential difference of each resistor. While in parallel combination potential difference is the same for each resistor but the current for the system is the sum of currents of each resistor.
Formula Used:
We are using the following formulae to solve the above-given problem:-
${{R}_{eq}}={{R}_{1}}+{{R}_{2}}.....+{{R}_{n}}$and $\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}....+\dfrac{1}{{{R}_{n}}}$.

Complete step-by-step solution:
For the resistances in series, we know that equivalent resistance of resistances is always greater than the greatest of individual resistance and the equivalent resistance in a parallel combination is always less than the value of the least individual resistance in the circuits.
In a series connection, the equivalent resistance is the sum of all the individual resistances and in a parallel connection, the reciprocal of equivalent resistance is the sum of reciprocal of the individual resistances.
We have the value of all three resistors as $6\Omega $.
Let the three resistors be ${{R}_{1}}, {{R}_{2}}$ and ${{R}_{3}}$.
Hence, ${{R}_{1}}={{R}_{2}}={{R}_{3}}=6\Omega $

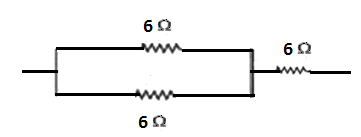
Connecting two resistors in parallel and one in series with the parallel ones we get
$\dfrac{1}{{{R}}} =\left( \dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}} \right)$
$\Rightarrow \dfrac{1}{{{R}}}=\left( \dfrac{1}{6}+\dfrac{1}{6} \right) $
$\Rightarrow \dfrac{1}{{{R}}}= \left( \dfrac{1+1}{6} \right)$
$\Rightarrow \dfrac{1}{{{R}}} = \left( \dfrac{2}{6} \right)$
$\Rightarrow R=3$
As the R in series with the ${{R}_{3}}$ we can use the reciprocal rule for the parallel combination
${{R}_{eq}}= R+{{R}_{3}} $
$\Rightarrow {{R}_{eq}}=3+6$
$\Rightarrow {{R}_{eq}}=9\Omega $.
Hence, to get the equivalent resistance of $9\Omega $ we have to connect two resistors in parallel and one in series with the parallel one.
Now for the second case, we have

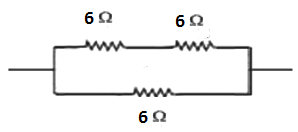
Connecting two resistors in series and one resistor in parallel to the series resistors we get
$R=\left( {{R}_{1}}+{{R}_{2}} \right)$
$\Rightarrow R=\left( 6+6 \right)$
$\Rightarrow R=12$
As ${{R}_{1}}$ and ${{R}_{2}}$ are in parallel with ${{R}_{3}}$ and using reciprocal rule for parallel connection we have
$\Rightarrow \dfrac{1}{{{R}_{eq}}}=\dfrac{1}{R}+\dfrac{1}{{{R}_{3}}} $
$\Rightarrow \dfrac{1}{{{R}_{eq}}} =\dfrac{1}{12}+\dfrac{1}{6}$
$\Rightarrow \dfrac{1}{{{R}_{eq}}}=\dfrac{3}{12}$
$\Rightarrow \dfrac{1}{{{R}_{eq}}} =\dfrac{1}{4}$
Again using the reciprocal rule for parallel combination we have
$ \Rightarrow {{R}_{eq}}=4\Omega $.
Therefore, to get the equivalent resistance of $4\Omega $we have to connect two resistors in series and one resistor in parallel to the series.

Note: In solving the problems related to equivalent resistance we should focus on the correct identification of the arrangements of resistances. We should not get confused between the formulae of series and parallel combinations. In a parallel combination, we have to find the reciprocal of each resistance.