Question

Show by section formula that the points (3, -2), (5, 2) and (8, 8) are collinear.

Answer 1

Hint:
1) The section formula gives the coordinates of a point P(x, y) which divides the line joining two points $A\left( {{x}_{1}},{{y}_{1}} \right)$ and $B\left( {{x}_{2}},{{y}_{2}} \right)$ in the ratio AP : PB = m : n, internally or externally.
2) For internal division: $P(x,y)=\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$ .
3) For external division: $P(x,y)=\left( \dfrac{m{{x}_{2}}-n{{x}_{1}}}{m-n},\dfrac{m{{y}_{2}}-n{{y}_{1}}}{m-n} \right)$ .
4) For three points $A\left( {{x}_{1}},{{y}_{1}} \right)$ , $B\left( {{x}_{2}},{{y}_{2}} \right)$ and $C\left( {{x}_{3}},{{y}_{3}} \right)$ to be collinear, the ratio m : n should be same in both ${{x}_{3}}=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n}$ and ${{y}_{3}}=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}$ .
i.e. $\dfrac{m}{n}=\dfrac{{{x}_{1}}-{{x}_{3}}}{{{x}_{3}}-{{x}_{2}}}=\dfrac{{{y}_{1}}-{{y}_{3}}}{{{y}_{3}}-{{y}_{2}}}$ .

Complete step by step solution:
Let's say that the points are $A\left( {{x}_{1}},{{y}_{1}} \right)=\left( 3,-2 \right)$ , $B\left( {{x}_{2}},{{y}_{2}} \right)=\left( 5,2 \right)$ and $C\left( {{x}_{3}},{{y}_{3}} \right)=\left( 8,8 \right)$ .
We know that, using the section formula, that for the points to be collinear: $\dfrac{m}{n}=\dfrac{{{x}_{1}}-{{x}_{3}}}{{{x}_{3}}-{{x}_{2}}}=\dfrac{{{y}_{1}}-{{y}_{3}}}{{{y}_{3}}-{{y}_{2}}}$ .
Here, $\dfrac{{{x}_{1}}-{{x}_{3}}}{{{x}_{3}}-{{x}_{2}}}=\dfrac{3-8}{8-5}=\dfrac{-5}{3}$ and $\dfrac{{{y}_{1}}-{{y}_{3}}}{{{y}_{3}}-{{y}_{2}}}=\dfrac{-2-8}{8-2}=\dfrac{-10}{6}=\dfrac{-5}{3}$.
Since both the values are the same, the points are collinear. Also, a negative value of $\dfrac{m}{n}=\dfrac{-5}{3}$ suggests that the point C is outside AB and the ratio AC : BC = 5 : 3.
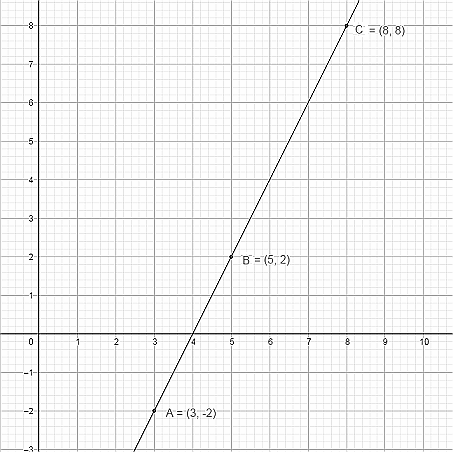
The position of the three points is shown below:

Note:
1) There are many ways to show that three points A, B and C are collinear (in a straight line):
2) Section formula (Ratio / Slope method).
3) Distance method: AB + BC = AC.
4) Area method: Area of Δ ABC = 0.