Question

Shape of graph between speed and kinetic energy of a body is-
(A). Hyperbola
(B). Straight Line
(C). Parabola
(D). Circle

Answer 1

Hint: Using the formula for kinetic energy, we determine the relationship between Kinetic energy and speed and analyse the dependent and independent variables out of the two. On the basis of whether the relationship is linear or polynomial we draw a graph and describe its characteristics.

Complete answer:
Speed is the distance travelled by a body in unit time. It’s SI unit is\[{\text{m}}/{\text{s}}\;\] .
\[\text{S = }\dfrac{\text{d}}{\text{t}}\]
Where d= distance traveled by a body in given time
t= time taken
Kinetic energy is the energy possessed by a body due to its motion. It can also be defined as the work required to accelerate a body from its rest position to given velocity. It’s SI unit is joules \[\text{(J)}\].
Kinetic Energy is given by-
\[\text{K = }\dfrac{\text{1}}{\text{2}}\text{m}{{\text{v}}^{\text{2}}}\] - (1)
Velocity varies continuously with time. eq (1) tells us about the relationship between Kinetic energy and speed. From this we can conclude that-
\[\text{K}\propto {{\text{v}}^{\text{2}}}\]
Here, \[\text{(}\dfrac{\text{1}}{\text{2}}\text{m)}\] is a constant.
The graph for a square relationship is a parabola. Eq of Parabola is-
\[{{\text{x}}^{\text{2}}}\text{ = 4ay}\] - (2)
Eq (1) is comparable to eq (2) and the graph will be-
       

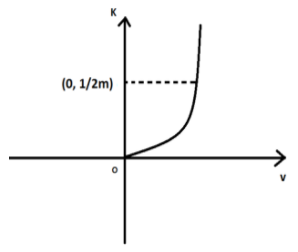
As the square of a variable cannot have negative values, the graph on the negative x-axis is absent.
As there is no intercept, the vertex of the parabola is at origin. Comparing eq (1) and eq (2), we get, \[\text{a = }\dfrac{\text{2}}{\text{m}}\] .Therefore the focus of parabola is at $(0, \dfrac{2}{m})$

Hence, the correct option is (C). Parabola

Note:
Here Kinetic Energy K , is the dependent variable and speed,is the independent variable. Therefore, by convention,K is taken along the y-axis and v is taken along the x-axis. Different parabolas can be formed depending on the axis of symmetry; here the axis of symmetry is the y-axis.