Question

Shanti sweets stall was placing an order for making cardboard boxes for packing their sweets. Two sizes of boxes were required. The bigger of dimensions 25 cm × 20 cm × 5 cm and the smaller of dimensions 15 cm × 12 cm × 5 cm. For all the overlaps, 5% of the total surface area is required extra. If the cost of the cardboard is Rs.4 for 1000 $c{{m}^{2}}$, find the cost of cardboard required for supplying 250 boxes of each kind.

Answer 1

Hint: To solve this question we will first find the total surface area of both the bigger box and the smaller box and after that we will find out the 5% extra area for each of the box and then add it with the total area. After finding the total area we will find the cost by multiplying the total area with 4 and dividing by 1000 as we are given that the cost of the cardboard is Rs.4 for 1000 $c{{m}^{2}}$.

Complete step-by-step answer:
We are given the dimensions of the bigger box as 25 cm × 20 cm × 5 cm,

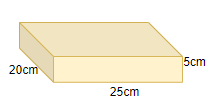
So it is a box with in the shape of cuboid so its total surface area will be given by,
Total Surface Area = $2\left( lb+bh+hl \right)$,
Where l = length, b = breadth, h = height of the cuboid so,
We get the area of the box with dimensions as 25 cm × 20 cm × 5 cm,
$=2\left( 25\times 20+20\times 5+5\times 25 \right)$
$\begin{align}
  & =2\left( 500+100+125 \right) \\
 & =2\left( 725 \right) \\
 & =1450c{{m}^{2}} \\
\end{align}$
Now we know that 5% extra area is required for each box so we get 5% as,
$\begin{align}
  & 5\%\,of\,1450c{{m}^{2}} \\
 & =\dfrac{5}{100}\times 1450 \\
 & =72.5c{{m}^{2}} \\
\end{align}$
So total area of the bigger box that is needed to make the box = 1450 + 72.5 = 1522.5$c{{m}^{2}}$
Now total area that is required for 250 such boxes we get as = $1522.5\times 250=380625c{{m}^{2}}$
Similarly, we will calculate the total surface area of smaller box with dimensions 15 cm × 12 cm × 5 cm,

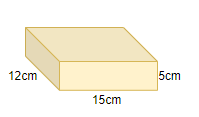
Total surface area = $2\left( 15\times 12+12\times 5+5\times 15 \right)$
$\begin{align}
  & =2\left( 180+60+75 \right) \\
 & =2\left( 315 \right) \\
 & =630c{{m}^{2}} \\
\end{align}$
For overlapping extra 5% area, so we get
$\begin{align}
  & =5\%\,of\,630 \\
 & =\dfrac{5}{100}\times 630 \\
 & =31.5c{{m}^{2}} \\
\end{align}$
Total area required for smaller box = $630+31.5=661.5c{{m}^{2}}$
Now total area that is required for 250 such boxes we get as = $250\times 661.5=165375c{{m}^{2}}$
Hence total area for both type of boxes is = $380625+165375=546000c{{m}^{2}}$
Now we are given that cost of 1000$c{{m}^{2}}$ sheet is Rs.4
So cost of 1$c{{m}^{2}}$ sheet we will get as $Rs.\dfrac{4}{1000}$
Hence cost of 546000$c{{m}^{2}}$ will be,
 $\begin{align}
  & Rs.\dfrac{4}{1000}\times 546000 \\
 & =Rs2184 \\
\end{align}$
Hence we get our answer as Rs.2184

Note: You should note that before calculating the amount you need to calculate the total area required for it before including the extra 5% area for each box, so try to read the question carefully before starting it to solve. And also while calculating the cost be careful as the cost for 1000$c{{m}^{2}}$ is given and not for 1$c{{m}^{2}}$, so first find out cost needed for 1$c{{m}^{2}}$ then proceed further.