
What is self-inductance? Establish expression for self-inductance of a long solenoid.
Answer
593.4k+ views
Hint: Self-inductance is the emf induced $e$ in a current carrying wire provided that the current $I$ is varying at a unity rate. In this we first start with the formula of magnetic flux density B that is $B = \dfrac{{{\mu _0}NI}}{l}$ then we substitute this in the equation of magnetic flux that is $\phi = BA$ and get$\phi = \dfrac{{{\mu _0}NI}}{l}A$. Now we equate $\phi = \dfrac{{{\mu _0}NI}}{l}A$ and $\phi = LI$. At last we get the required expression for self-inductance of a long solenoid as $L = \dfrac{{{\mu _0}NA}}{l}$.
Complete Step-by-Step solution:
Self-inductance is the emf induced $e$ or the voltage induces in a current-carrying wire provided that the current $I$ in the wire is varying at a unit rate that is $\dfrac{{dI}}{{dt}} = 1$. The expression for self-inductance $L$ is given as:
$L = \dfrac{e}{{\dfrac{{dI}}{{dt}}}}$------------------------------------- (1)
When $\dfrac{{dI}}{{dt}} = 1$ we get $L = e$. Its S.I unit is henry (H).
Now let us assume a long solenoid of length l, radius r, and the number of turns equal to N as shown in figure 1. Current $I$ flowing through the solenoid. The flux development is $\phi $ and the emf induced due to this varying current is $e$.
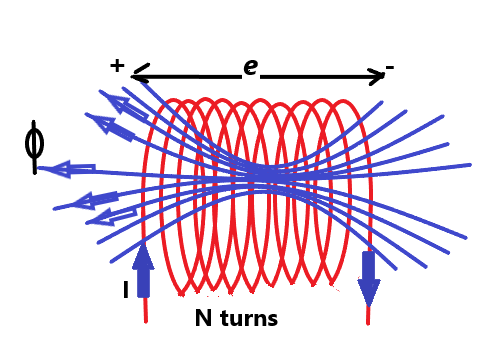
Now we know the formula for magnetic flux density is
$B = \dfrac{{{\mu _0}NI}}{l}$---------------------------------- (2)
Where B is magnetic flux density in tesla
${\mu _0}$ is the permeability of free space
We also know that the expression for magnetic flux is
$\phi = BA$------------------------------------ (3)
Where A is the cross-section area of the solenoid which is equal to $\pi {r^2}$. Now substituting equation number (2) in equation number (1) we will get
$\phi = \dfrac{{{\mu _0}NI}}{l}A$---------------------------------- (4)
There is another expression for the flux magnetic that is:
$\phi = LI$-------------------------------------- (5)
Therefore, by equating equation (4) and equation (5) we will get
$LI = \dfrac{{{\mu _0}NI}}{l}A$
$ \Rightarrow L{I} = \dfrac{{{\mu _0}N{I}}}{l}A$
$ \Rightarrow L = \dfrac{{{\mu _0}NA}}{l}$
Hence the expression for self-inductance of a long solenoid is $L = \dfrac{{{\mu _0}NA}}{l}$
Note: For these types of questions we need to have a clear understanding of electric field intensity E, electric flux density D, Magnetic field intensity H, magnetic flux density B, and magnetic flux $\phi $. We need to know the expression for self-inductance and mutual-inductance when there is a solenoid, current-carrying wire, or a toroid.
Complete Step-by-Step solution:
Self-inductance is the emf induced $e$ or the voltage induces in a current-carrying wire provided that the current $I$ in the wire is varying at a unit rate that is $\dfrac{{dI}}{{dt}} = 1$. The expression for self-inductance $L$ is given as:
$L = \dfrac{e}{{\dfrac{{dI}}{{dt}}}}$------------------------------------- (1)
When $\dfrac{{dI}}{{dt}} = 1$ we get $L = e$. Its S.I unit is henry (H).
Now let us assume a long solenoid of length l, radius r, and the number of turns equal to N as shown in figure 1. Current $I$ flowing through the solenoid. The flux development is $\phi $ and the emf induced due to this varying current is $e$.

Figure 1
Now we know the formula for magnetic flux density is
$B = \dfrac{{{\mu _0}NI}}{l}$---------------------------------- (2)
Where B is magnetic flux density in tesla
${\mu _0}$ is the permeability of free space
We also know that the expression for magnetic flux is
$\phi = BA$------------------------------------ (3)
Where A is the cross-section area of the solenoid which is equal to $\pi {r^2}$. Now substituting equation number (2) in equation number (1) we will get
$\phi = \dfrac{{{\mu _0}NI}}{l}A$---------------------------------- (4)
There is another expression for the flux magnetic that is:
$\phi = LI$-------------------------------------- (5)
Therefore, by equating equation (4) and equation (5) we will get
$LI = \dfrac{{{\mu _0}NI}}{l}A$
$ \Rightarrow L{I} = \dfrac{{{\mu _0}N{I}}}{l}A$
$ \Rightarrow L = \dfrac{{{\mu _0}NA}}{l}$
Hence the expression for self-inductance of a long solenoid is $L = \dfrac{{{\mu _0}NA}}{l}$
Note: For these types of questions we need to have a clear understanding of electric field intensity E, electric flux density D, Magnetic field intensity H, magnetic flux density B, and magnetic flux $\phi $. We need to know the expression for self-inductance and mutual-inductance when there is a solenoid, current-carrying wire, or a toroid.
Recently Updated Pages
Two men on either side of the cliff 90m height observe class 10 maths CBSE

What happens to glucose which enters nephron along class 10 biology CBSE

Cutting of the Chinese melon means A The business and class 10 social science CBSE

Write a dialogue with at least ten utterances between class 10 english CBSE

Show an aquatic food chain using the following organisms class 10 biology CBSE

A circle is inscribed in an equilateral triangle and class 10 maths CBSE

Trending doubts
The shortest day of the year in India

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the missing number in the sequence 259142027 class 10 maths CBSE




