Question

See Fig. and write the following:

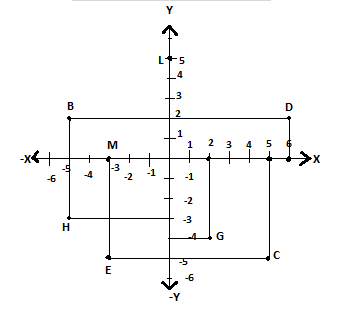
I.The Coordinates of B.
II.The Coordinates of C.
III.The point identified by the coordinates (-3,-5)
IV.The point identified by the coordinates (2,-4)
V.The abscissa of the point D.
The ordinate of the point H.
VI.The coordinates of the point L.
VII.The coordinates of the point M.

Answer 1

Hint: Abscissa is the horizontal or the x-coordinate of a point in a two-dimensional system of Cartesian coordinates. It is the distance measured from the y-axis parallel to the x-axis, whereas ordinate is the y-coordinates of a point into a two-dimensional system of Cartesian coordinates. It is the distance measured from the x-axis parallel to the y-axis
The term coordinate represents the position of the given point along the line, arc, and so on, whereas the term ordinate represents the value of a coordinate on the y-axis.
In this question, to find the coordinates of the given points, find the abscissa and the ordinate of each point and then find their coordinates. The co-ordinates of every point is written as (abscissa,ordinate)

Complete step-by-step answer:
I.The Coordinates of B.
Observe point B, where
Abscissa= x-coordinate\[ = - 5\]
Ordinate =y-coordinate \[ = 2\]
Hence, Coordinate\[ = B\left( { - 5,2} \right)\]

II.The Coordinates of C.
Observe point C, where
Abscissa= x-coordinate\[ = 5\]
Ordinate =y-coordinate \[ = - 5\]
Hence, Coordinate\[ = C\left( {5, - 5} \right)\]

III.The point identified by the coordinates (-3,-5)
From the given coordinate \[\left( { - 3, - 5} \right) \to \left( {x,y} \right)\]
X-coordinate= Abscissa\[ = - 3\]
Y-coordinate= Ordinate \[ = - 5\]
Hence the point is E.

IV.The point identified by the coordinates (2,-4)
From the given coordinate \[\left( {2, - 4} \right) \to \left( {x,y} \right)\]
X-coordinate= Abscissa \[ = 2\]
Y-coordinate= Ordinate \[ = - 4\]
Hence the point is G

V.The abscissa of the point D
Abscissa= x-coordinate\[ = 6\]
Hence the abscissa of point D= 6
The ordinate of the point H
Ordinate= y-coordinate\[ = - 3\]
        Hence the Abscissa of point H\[ = - 3\]

VI.The coordinates of the point L.
Observe the point L, where
        Abscissa= x-coordinate\[ = 0\]
        Ordinate =y-coordinate \[ = 5\]
         Hence, Coordinate\[ = L\left( {0,5} \right)\]

VII.The coordinates of the point M
Observe the point M, where
Abscissa= x-coordinate\[ = - 3\]
        Ordinate =y-coordinate \[ = 0\]
        Hence, Coordinate\[ = M\left( { - 3,0} \right)\]

Note: One of the easy methods to find the coordinate of a point is by counting the interval from the origin on the x-axis and the y-axis, and the interval on which the point lies on the x-axis is abscissa, and the point on the y-axis is ordinate. In some cases, the scale of the interval is also considered.