Question

Say true or false of the following statement.
The statement is, Two diameters of a circle will necessarily intersect
\[{\text{A}}{\text{.}}\] True
${\text{B}}{\text{.}}$ False

Answer 1

Hint: Here we go through by first making the diagram of a circle and then make two different diameters in the circle then analyze the diameter whether they intersect or not.

As we know the definition of a circle is a shape consisting of all points in a plane that are a given distance from a given point, the center; equivalently it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant.

And the diameter says a line segment whose endpoints lie on the circle and that passes through the center; this is the largest distance between any two points on the circle.

As we know from the above definition the diameter always passes through the center. And the line segment which joins center to the point on circumference is known as radius.

Now in the figure there are two diameters AB and CD which are passing through center O.

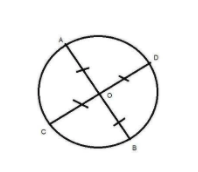
And we can say the line segments OA, OB, OC and OD are the radius of the circle.

So we can say that diameter=2$ \times $radius.

Hence the center bisects the diameter into two parts which are known as radius.

So we can say that the statement is true.

Hence option A is the correct answer.

Note: Whenever we face such a type of a question the key concept for solving the question is you have to remember the definition of all the terms that are used in the question. By the help of these definitions you can easily get the answer.