Question

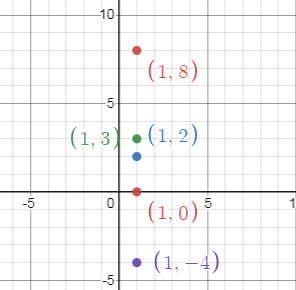
What can you say about the positions of the points \[\left( {1,2} \right)\], \[\left( {1,3} \right)\], \[\left( {1,{\text{ }} - 4} \right)\], \[\left( {1,0} \right)\] and \[\left( {1,8} \right)\]. Locate them on graph.

Answer 1

Hint: Any point on the Cartesian system is denoted as (x, y) where x is the x coordinate and y is the y coordinate.
The coordinate - axis divides the cartesian plane into four Quadrants.
In the First - Quadrant, both x-coordinate and y-coordinate are positive, i.e., the points on the first - quadrant are (x, y).
In the Second - Quadrant x-coordinate is negative and the y-coordinate is positive, i.e., the points on the second - quadrant are (-x, y).
In the third Quadrant, both x-coordinate and y-coordinate are negative, i.e., the points on the third quadrant are (-x, -y).
In the Fourth -Quadrant x-coordinate is positive while the y-coordinate is negativities, the points on the fourth quadrant are (x, -y).
Any point lying on the x-axis has coordinates of the form (x, 0).
Any point lying on the y-axis has coordinates of the form (0, y).

Complete step by step answer:
The point \[\left( {1,2} \right)\] lies in the first quadrant because both x and y-coordinate are positive.
Here both the coordinates are greater than zero. So we can say that the point lies in the first quadrant.
The point \[\left( {1,3} \right)\] lies in the first quadrant because both x and y-coordinate are positive.
Here we can able to say that both the coordinates are greater than zero. So we can say that the point lies in the first quadrant.
The point \[\left( {1,{\text{ }} - 4} \right)\] lies in the fourth quadrant because the x-coordinate is positive and the y-coordinate is negative.
Here the x-coordinate is greater than zero and the y-coordinate is less than zero. So, the above point lies in the fourth quadrant.
The point \[\left( {1,0} \right)\] lies on the x-axis because y-coordinate is zero.
If the given point is of the form $\left( {x,0} \right)$ , then the point will lie on the x-axis for all $x \in \mathbb{R}$
The point \[\left( {1,8} \right)\] lies in the first quadrant because both x and y-coordinate are positive.
Here we can note that both the coordinates are greater than zero. So we can say that the point lies in the first quadrant.

Note:
We can also able to calculate the quadrants for the trigonometry values. Remind that the given quadrant functions are two-dimensional only.
The other one is three-dimensional with the axis points of three variables respectively to $x,y,z$.