Question

What do you say about the line which is perpendicular to the radius of the circle through the point at circumference?

Answer 1

Hint: The incredible number and variety of circumstances in science where circles are used to model physical phenomena reflects their theoretical significance. Theorems of circle geometry are not intuitively apparent to students; in fact, most people are shocked when they first see the results.

Complete step-by-step answer:
Tangent to the circle is a line that is perpendicular to the radius of the circle and passes through the point at the circumference. Actually it is said to be a tangent is a straight line drawn from an external point that touches the circumference of a circle at exactly one point. So it is commonly said that a circle can have an infinite number of tangents. These tangents have certain properties that can be used to perform mathematical computations on circles using identities.
So actually it is said to be a tangent to a circle is a line that only intersects the circle once. It is possible that the line is a secant, splitting the circle in two places. The line could be a tangent, just touching the circle once. It is possible that the line would completely skip the circle.
A point of contact is the point where a tangent meets a circle. It is not immediately clear how to draw a tangent at a specific point on a circle, or even whether there are several tangents at that point.
A circle's radius is perpendicular to the tangent line passing through its endpoint on the circumference. A tangent line, on the other hand, is the perpendicular to a radius passing through the same endpoint. The geometrical figure of a circle and tangent line that results has reflection symmetry around the radius axis.

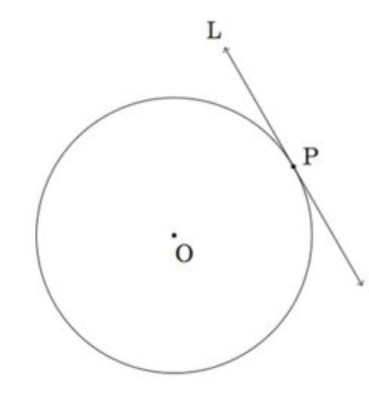
So, the correct answer is “TANGENT”.

Note: The terms ‘secant' and 'tangent' are both Latin words that mean 'cutting' (as in 'cross-section') and 'touching' (as in 'tango'). The graph of the affine function that best approximates the original function at the given point can also be thought of as the tangent line to a point on a differentiable curve.