Question

Sajal can ride a scooter constantly at a speed of \[30Km/hr\]. Draw a distance-time graph for the situation: The time taken by Sajal to ride 75 Km.

Answer 1

Hint: We draw a distance-time graph depicting speed of scooter. Using a unitary method we calculate the distance covered after several hours and plot the points on the graph. We calculate the time taken by Sajal to ride given distance using the formula of time in terms of speed and distance covered.
* If distance ‘d’ is covered in time ‘t’ with speed ‘s’ then we have the formula for speed as \[s = \dfrac{d}{t}\]
Shift ‘t’ to the numerator in LHS and shift ‘s’ to the denominator in RHS we get formula for time taken i.e. \[t = \dfrac{d}{s}\]

Complete step by step answer:
We are given that speed of scooter is \[30Km/hr\]
\[ \Rightarrow \]Distance covered in 1 hour \[ = 30\]Km
Let us take distance covered on the x-axis and time taken on y-axis.
Denote distance by ‘x’ and time taken by ‘y’
When\[x = 30\], then\[y = 1\]
\[ \Rightarrow x = 30,y = 1\] … (1)
When\[x = 2 \times 30\], then \[y = 2 \times 1\]
\[ \Rightarrow x = 60,y = 2\] … (2)
When\[x = 0.5 \times 30\], then \[y = 0.5 \times 1\]
\[ \Rightarrow x = 15,y = 0.5\] … (3)
When\[x = 1.5 \times 30\], then \[y = 1.5 \times 1\]
\[ \Rightarrow x = 45,y = 1.5\] … (4)
We draw a graph depicting the speed, having distance on the x-axis and time on the y-axis.
From equations (1), (2), (3) and (4), we can write the points in\[(x,y)\]form
Points on the graph are \[(0.5,15);(1,30);(1.5,45);(2,60)\]

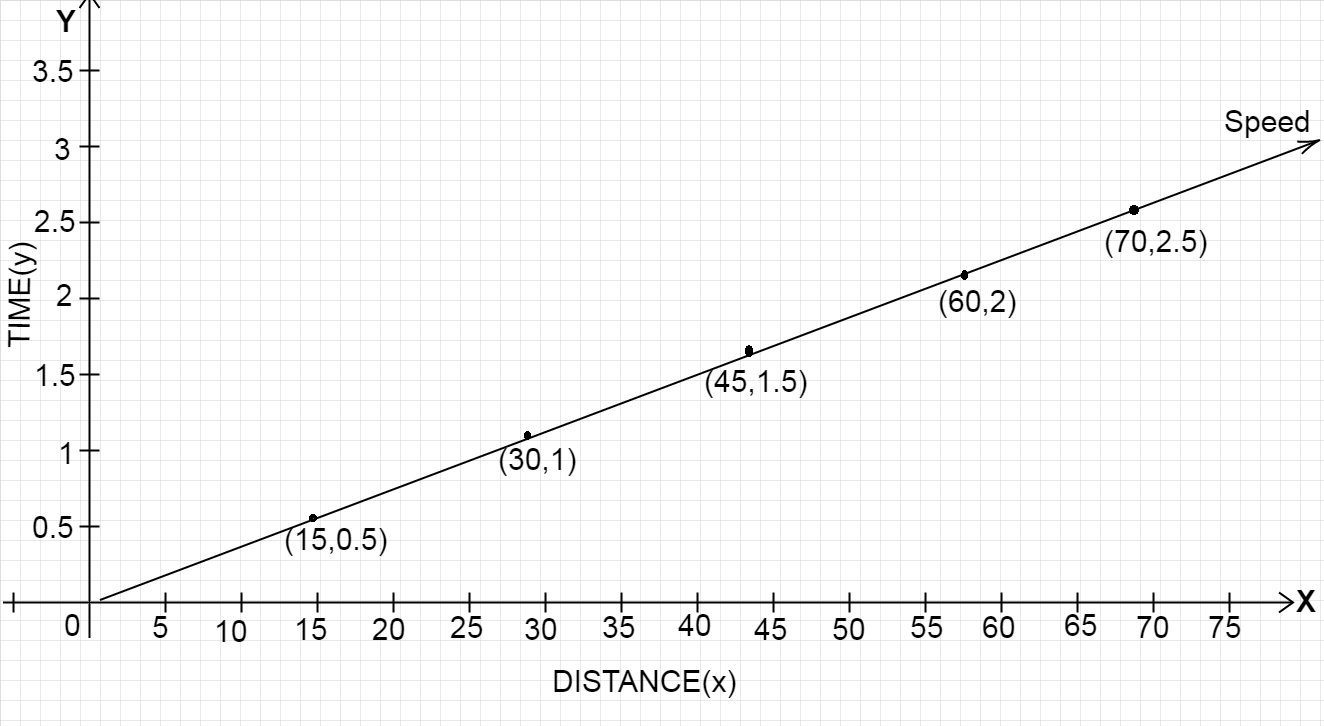
Now we have to find the time taken by Sajal to ride 75 Km.
We calculate the time taken by Sajal to ride using the formula of time i.e. \[t = \dfrac{d}{s}\], where ‘t’ denotes the time, ‘d’ denotes the distance and ‘s’ denotes the speed
We are given speed of scooter as \[30Km/hr\]
\[ \Rightarrow s = 30\]
Also, distance travelled is given to be 75 Km
\[ \Rightarrow d = 75\]
Substitute the value of \[s = 30,d = 75\] in the formula of time
\[ \Rightarrow t = \dfrac{{75}}{{30}}\]
Cancel of same terms from numerator and denominator
\[\Rightarrow t = 2.5\]

\[\therefore \] The time taken to travel 75 Km is 2.5 hours.

Note:
Alternate method:
We can calculate time taken using unitary method
Unitary method helps us to find the value of multiple units when given the value of a single unit by multiplying the value of a single unit by the number of units.
We know time taken by Sajal to travel 30 Km \[ = 1\]hour
\[ \Rightarrow \]Time taken by Sajal to travel 1 Km \[ = \dfrac{1}{{30}}\]hour
\[ \Rightarrow \]Time taken by Sajal to travel 75 Km \[ = \left( {\dfrac{1}{{30}} \times 75} \right)\]hour
Cancel same factors from numerator and denominator
\[ \Rightarrow \]Time taken by Sajal to travel 75 Km \[ = 2.5\]hour

\[\therefore \]The time taken to travel 75 Km is 2.5 hours.