Question

Sachin (S) hits a ball along the ground with a speed \[u\] in a direction which makes an angle \[30{}^\circ \] with the line joining him and the fielder Prem (P). Prem runs to intercept the ball with a speed \[\dfrac{2u}{3}\]. At what angle should he run to intercept the ball?
A. \[{{\operatorname{Sin}}^{-1}}\left[ \dfrac{\sqrt{3}}{2} \right]\]
B. \[{{\operatorname{Sin}}^{-1}}\left[ \dfrac{2}{3} \right]\]
C. \[{{\operatorname{Sin}}^{-1}}\left[ \dfrac{3}{4} \right]\]
D. \[{{\operatorname{Sin}}^{-1}}\left[ \dfrac{\sqrt{4}}{5} \right]\]

Answer 1

Hint: Given that, the ball was hit with a speed \[u\].The ball makes an angle \[30{}^\circ \] with the line joining Sachin and the fielder. Since the velocity is a vector quantity, it can be split into its horizontal and vertical components. Using a diagram we can determine the components of the ball velocity vector and fielder velocity vector. The sin component of the ball velocity should be equal so to the sin component of the velocity of the fielder.
Formula used:
\[\vec{v}={{v}_{x}}+{{v}_{y}}=v\sin \theta +v\cos \theta \]

Complete answer:
Given that,
\[\text{Speed of ball = u}\]
\[\text{Angle }\!\!~\!\!\text{ of ball = 30}{}^\circ \]
\[\text{Velocity of fielder =}\dfrac{\text{2u}}{\text{3}}\]
Let’s find the components of the velocity vector.
If velocity vector \[\vec{v}\] makes an angle \[\text{ }\!\!\theta\!\!\text{ }\] with y axis and has its horizontal and vertical components in x and y axis, then, velocity \[\vec{v}\] can be resolved into,
\[\vec{v}={{v}_{x}}+{{v}_{y}}=v\sin \theta +v\cos \theta \]
 

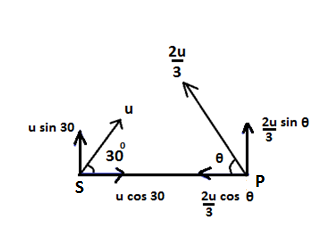
Components of velocity of ball are, \[\text{u sin 30, u cos 30}\].
Components of velocity of fielder are, \[\dfrac{\text{2u}}{\text{3}}\text{ sin }\!\!\theta\!\!\text{ , }\dfrac{\text{2u}}{\text{3}}\text{cos }\!\!\theta\!\!\text{ }\]
Here, to intercept the ball with the fielder, the vertical components of ball’s velocity and fielder’s velocity should be equal.
\[\text{u sin 30}=\dfrac{2u}{3}\text{sin }\theta \] -------- 1
We have, \[\text{sin 30}=\dfrac{1}{2}\] ----------- 2
Substitute 2 in equation 1. We get,
\[\text{u }\times \dfrac{1}{2}=\dfrac{2u}{3}\text{sin }\theta \]
\[\dfrac{1}{2}=\dfrac{2u}{3}\text{sin }\theta \]
\[\text{sin }\theta =\dfrac{3}{4}\]
\[\theta =\text{sin}{{\text{ }}^{-1}}\left( \dfrac{3}{4} \right)\]

So, the correct answer is “Option C”.

Additional Information:
A vector is a quantity that has both magnitude and direction. Force, displacement, Velocity and acceleration are some of the vector quantities. A vector quantity can be represented as,
\[\vec{v}=\left( {{v}_{x}},{{v}_{y}} \right)\]
In a 2D coordinate system, a vector quantity is broken into its x component and y component.
 

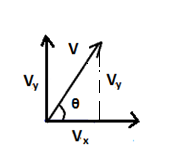
The trigonometric ratio of vectors gives the relation between components of vectors and magnitude of vectors. Using a triangle, we can derive the trigonometric ratios of a vector. Consider \[{{\text{v}}_{\text{x}}}\text{,}{{\text{v}}_{\text{y}}}\text{ and v}\] as the three sides of triangle. If \[\theta \]is the angle between \[{{\text{v}}_{\text{x}}}\text{ and v}\].Then,
\[\cos \theta =\dfrac{\text{adjacent side}}{\text{Hypotenuse}}=\dfrac{{{v}_{x}}}{v}\]
\[\sin \theta =\dfrac{\text{opposite side}}{\text{Hypotenuse}}=\dfrac{{{v}_{y}}}{v}\]
\[{{v}_{x}}=v\text{ cos}\theta \]
\[{{v}_{y}}=v\text{ sin}\theta \]
Using Pythagoras Theorem,
\[\left| {\vec{v}} \right|=\sqrt{v_{x}^{2}+v_{y}^{2}}\]

Note:
While resolving a vector into its horizontal and vertical components, remember that the component adjacent to the angle goes with the cosine; the component opposite to the angle goes with the sin. If the vector has a direction towards northeast, then it has sin and cosine components in north and east directions respectively, and if a vector is directing towards south west, its sin and cosine components are in south and west directions respectively.