Question

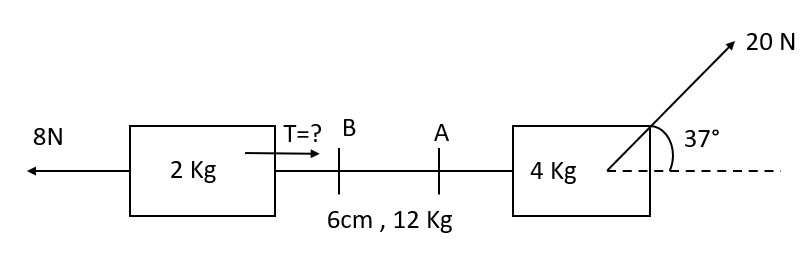
When rope has mass $12$ Kg, find the tension shown in figure.

Answer 1

Hint: Tension is a force adjacent to the length of a medium, particularly a force provided by flexible means, such as a rope or wire. The word "tension" originates from a Latin word signifying "to stretch." We apply Newton's second law to describe the motion of the object to the forces concerned.


Complete step-by-step solution:
Given: $m_{1} = 2 Kg$; $m_{2} = 4 Kg$
Mass of rope, $m_{r} = 12 Kg$
Total mass of the system $= m_{1} + m_{2} + m_{r}$
$m_{total}= 2 + 4 + 12 = 18 Kg$
Apply Newton’s second law in the whole system:
$20 cos 37^{\circ} – 8 = m_{total} \times a$
$\implies 20 cos 37^{\circ} – 8 = 18 \times a$
$\implies 7.97 = 18a$
$a = 0.44 ms^{-2}$
Now we apply Newton’s second law around $m_{1}$ .
Total mass of the system, $m_{s1} = 2 + 4 = 6 Kg$
$T – 8 = m_{s1} \times a$
$\implies T – 8 = 6 \times 0.44$
$\implies T – 8 = 2.64$
$\implies T = 10.64 N$
The tension is $10.64 N$.

Note:Tension, as an action-reaction pair of forces, as a transmitted force, or as restoring strength, may be a force and has the force units estimated in newtons. The ends of a string will apply forces on the objects to which the string is attached in the way of the string at the attachment point.