Question

Rock faults are ruptures along which opposite faces of rock have slid past each other. In Fig. 3-35, points A and B coincided before the rock in the foreground slid down to the right. The net displacement AB is along the plane of the fault. The horizontal component of AB is the strike-slip AC. The component of AB that is directed down the plane of the fault is the dip-slip AD.
(a) What is the magnitude of the net displacement AB if the strike-slip is 22.0 m and the dip-slip is 17.0 m? (b) If the plane of the fault is inclined at angle $\phi = {52^ \circ }$ to the horizontal, what is the vertical component of AB?

Answer 1

Hint: The given question is of the basic vector system. To solve this question, we need to be clear about vectors and the formulas linked with vectors. Resultant vector and vector substitution is all required to understand and solve the question.

Complete step by step answer:
Vectors are the quantities that have magnitude as well as direction. Though the question is stated in 3-D but we can imagine the problem in 2-D as the main vectors acting are in 2-D with each other.Resultant vector is the vector sum of the vectors which is basically the point or position or direction in which the combined action of all vectors occurs.

(a) If we look upon the question, we can draw out the following picture of strike-slip and dip-slip with net displacement as:

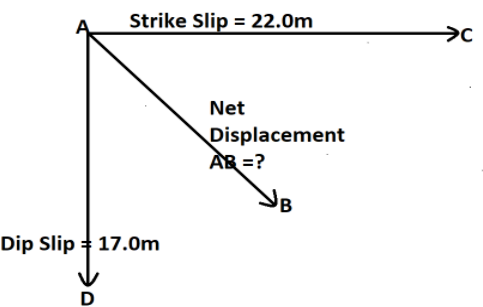
Net displacement is the resultant of dip-slip vector and strike-slip vector which is evaluated as,
${\text{Net displacement = }}\left| {\overrightarrow {{\text{AB}}} } \right| = \sqrt {{{\left| {{\text{AD}}} \right|}^2} + {{\left| {{\text{AC}}} \right|}^2}} $
Putting the values of variables from question,
$\left| {\overrightarrow {{\text{AB}}} } \right| = \sqrt {{{\left( {17.0{\text{m}}} \right)}^2} + {{\left( {22.0{\text{m}}} \right)}^2}} $
Evaluating the above equation,
$\left| {\overrightarrow {{\text{AB}}} } \right| = 27.8{\text{m}}$

Therefore, magnitude of net displacement of dip-slip and strike-slip is $\left| {\overrightarrow {{\text{AB}}} } \right| = 27.8{\text{m}}$.

(b) Now according to the question, we have been provided with the horizontal angle of AB vector and the value of its vertical component is being asked.Any vector, on substitution yields two components. One is the cos component and the other is the sin component. The component which is along the angle forms the cos component of vector and one which is away from angle forms the sin component as demonstrated below:

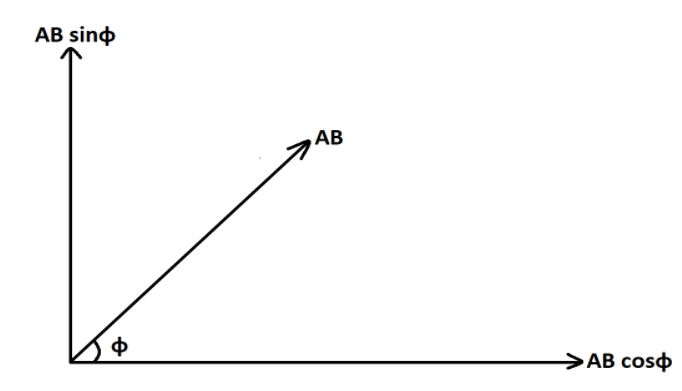
As we have been provided with horizontal angle and is asked for vertical component, hence the vertical component of net displacement (let x) is,
$x = AB\sin \phi $
Putting value of $\phi $ from question and of AB from the last part,
$x = 27.8\sin ({52^ \circ })$
Calculating the equation will give,
x = 13.4m

Therefore, the vertical component of net displacement is x = 13.4 m.

Note: We must never forget the basics behind every topic. Sometimes the statement of question provides a whole difficult identity of the question but the answer may lay behind the basic methodology only. We must also try to draw vectors or imagine it well so that we can understand the situation in a much better way.