Question

How do you rewrite $y + 2 = 4\left( {x - 3} \right)$ in slope intercept form?

Answer 1

Hint: In this question, we have to make a given equation in the form of slope intercept form of a line. It can be done by first simplifying $4\left( {x - 3} \right)$ by applying the distributive property. Next, move all terms not containing $y$ to the right side of the equation. For this, subtract $2$ from both sides of the equation. The equation obtained will be the equation of the given line in slope intercept form.

Formula used:
The Slope Intercept Form of a Line:
The equation of a line with slope $m$ and making an intercept $c$ on $y$-axis is $y = mx + c$.

Complete step by step solution:
We know that the slope intercept form of a line is the equation of a line with slope $m$ and making an intercept $c$ on $y$-axis is $y = mx + c$.
Given equation is $y + 2 = 4\left( {x - 3} \right)$
So, we have to make a given equation in the form of $y = mx + c$, the equation of a line with slope $m$ and making an intercept $c$ on $y$-axis.
First, simplify $4\left( {x - 3} \right)$ by applying the distributive property.
$ \Rightarrow y + 2 = 4x - 12$
Now, move all terms not containing $y$ to the right side of the equation.
For this, subtract $2$ from both sides of the above equation.
$ \Rightarrow y = 4x - 12 - 2$
$ \Rightarrow y = 4x - 14$
Now, compare this equation with the standard slope intercept form of a line and find the slope $m$ and an intercept $c$ on $y$-axis for this equation.
Here, $m = 4$ and $c = - 14$.

Therefore, $y + 2 = 4\left( {x - 3} \right)$ in slope intercept form is $y = 4x - 14$.

Note: Slope and $y$-intercept of a line can also be determined by graphing the given equation.
Graph of $y + 2 = 4\left( {x - 3} \right)$:

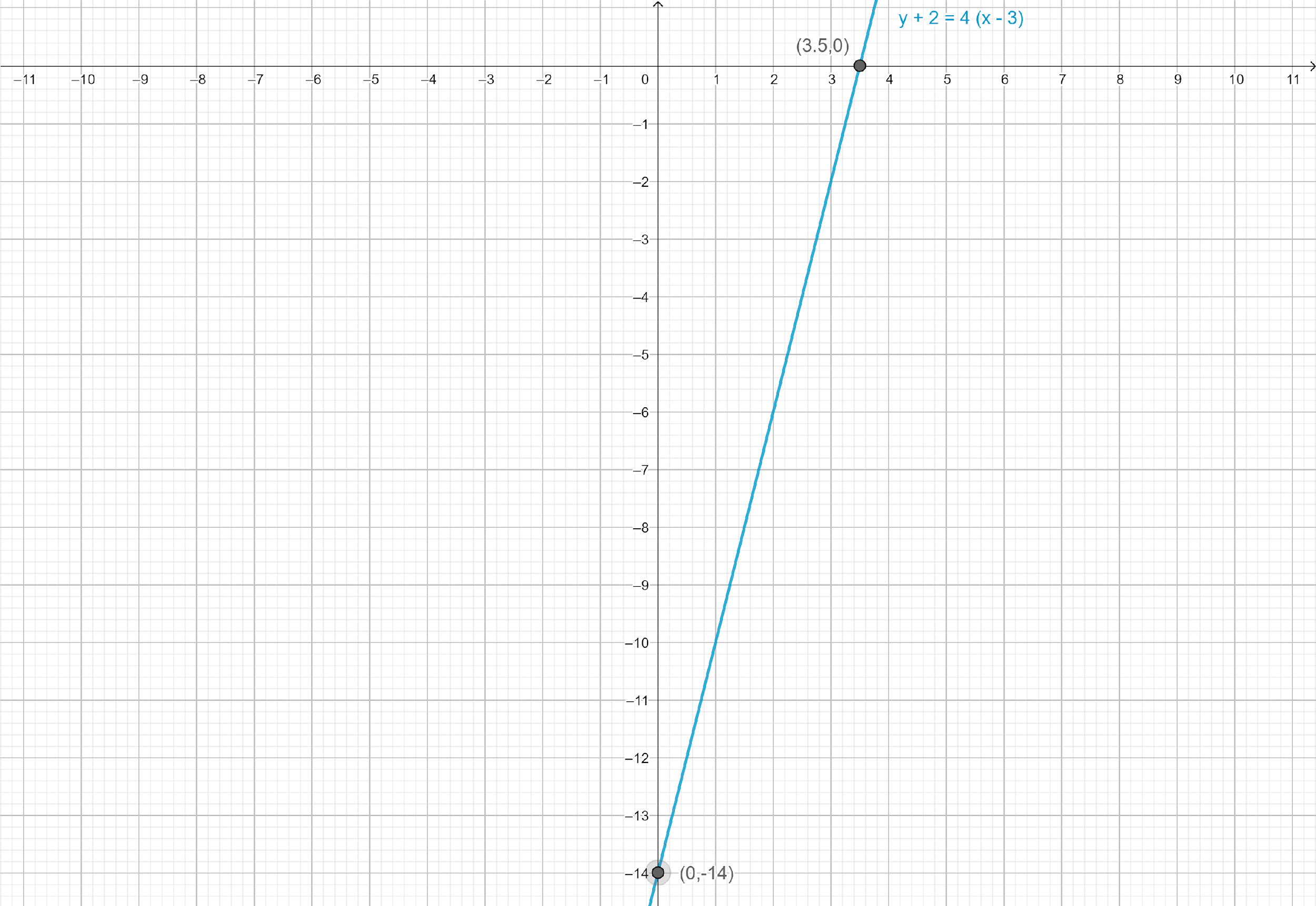
Since, the line $y + 2 = 4\left( {x - 3} \right)$ cuts the $y$-axis at $ - 14$.
So, $y$-intercept of a given line is $ - 14$.
$ \Rightarrow c = - 14$
We can find the slope of given line by putting $\left( {{x_1},{y_1}} \right) = \left( {3.5,0} \right)$ and $\left( {{x_2},{y_2}} \right) = \left( {0, - 14} \right)$ in $m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$.
So, slope is
$m = \dfrac{{ - 14 - 0}}{{0 - 3.5}}$
On simplification, we get
$m = 14 \times \dfrac{{10}}{{35}}$
$ \Rightarrow m = 4$
So, the slope of the given line is $4$.
Now, put the value of $m$ and $c$ in $y = mx + c$.
$ \Rightarrow y = 4x - 14$
Final solution: Therefore, $y + 2 = 4\left( {x - 3} \right)$ in slope intercept form is $y = 4x - 14$.