Question

What is the resultant of three coplanar forces: \[300N\] at \[0^\circ \] , \[400N\] at \[30^\circ \] , \[400N\] at \[150^\circ \] ?

Answer 1

Hint: For a two-dimensional vector, it can be split into two components. If the vector is in the x=y plane, it can be split into its x and y components. Considering vector $A$ having two components, its x component will be \[{A_x} = A\cos \theta \] and the y component will be \[{A_y} = A\sin \theta \].

Formulas used:
\[A = {\left( {A\sin \theta } \right)^2} + {\left( {A\cos \theta } \right)^2}\]
Addition of two vectors $a$ and $b$ are,
\[\sqrt {{a^2} + {b^2} + ab\cos \theta } \]
where \[\theta \] is the angle between the two vectors.

Complete step by step answer:

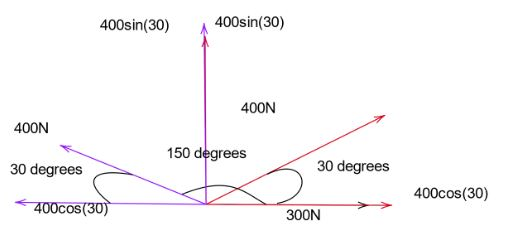
Let us consider three vectors as shown in the figure above. Let us assume their names to be their colors, black, red and blue. Black is not split into its respective components because it is aligned with the x-axis. The value of black is \[300N\].

Red is split into two components as shown, \[400\sin \left( {30} \right)\] and \[400\cos \left( {30} \right)\]. Blue is also split into two components but, since blue is closer to the negative x-axis, we take \[\left( {180 - \theta } \right)\] instead of \[\theta \]. Now the $x$ component of red and $x$ component of blue gets canceled as they are of equal magnitude but are in the opposite direction. Leaving us with

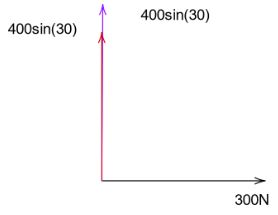
The two vectors each of value \[400\sin \left( {30} \right)\] get added up to \[2 \times 400\sin (30)\]. Since both of the vectors are in the same direction, we directly add and resulting in a vector in the y-direction whose magnitude will be: \[400N\]
(Since the value of \[\sin (30) = \left( {\dfrac{1}{2}} \right)\] and \[2 \times 400 = 800\] )

Now we are left with two vectors, one with a magnitude of \[300N\] in the direction of the x-axis and the other with a magnitude of \[400N\] along the direction of the y axis.The resultant can be found out using the formula:
\[\sqrt {{a^2} + {b^2} + ab\cos \theta } \]
The resultant of the addition will be:
\[\sqrt {{{300}^2} + {{400}^2} + 300 \times 400 \times \cos (90)} = 500N\]

Therefore, the resultant of three coplanar forces: \[300N\] at \[0^\circ \] , \[400N\] at \[30^\circ \] , \[400N\] at \[150^\circ \] will be \[500N\].

Note: The splitting of the forces into their respective components is very important.The cancellation of the components having equal magnitude but in the opposite direction must be carried properly. This is done because the values are equal but in the opposite directions. Any vector can be resolved into an infinite number of components, but we resolve it into the rectangular components only to form simpler equations for the sake of our convenience.