Question

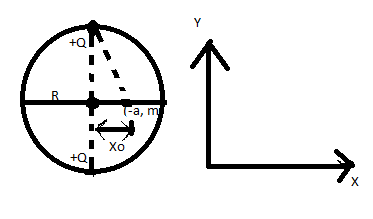
What is the resultant force acting on the charged bead?

Answer 1

Hint: First we have to label the points on the bead and then find the cosine of the angle between the points on the axes and the midpoint. Then we can find the resultant force and then observe what type of force is acting on the charged bead.

Complete step by step solution:

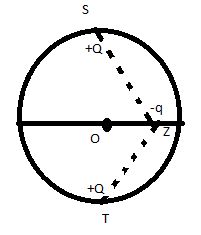
Let us consider O as the mid-point and points S and T acting along the y-axis and Z on the x-axis.
The positive charge at S will attract the negative charge at point Z and S will pull Z towards itself.
Similarly the positive charge at T will pull the negative charge Z towards itself.
Now, let us consider two forces ${F_1}$ acting along SZ and ${F_2}$ acting along TZ.
These two forces will have their components around ZO and the perpendicular to the ZO in the opposite directions, respectively.
If we consider the magnitudes of the forces both ${F_1}$ and ${F_2}$ are equal.
The perpendicular elements are cancelled and the components are added together with ZO.
Now we find the cosine of the angles formed.
The cosine of angle SZO is $\dfrac{{OZ}}{{SZ}}$
The cosine of angle TZO is $\dfrac{{OZ}}{{TZ}}$

So, the resultant forces is given by $ = \dfrac{{{F_1} \times OZ}}{{SZ}} + \dfrac{{{F_2} \times OZ}}{{TZ}}$

If we observe the diagram in the question we can see that ${X_0} < < R$, OZ is insignificant and becomes nearly zero for the value of the calculated force.

Hence, we can say that the force acting along the bead is negligible unbalanced force.

Note: At last we find that the forces acting along the bead are not equal in magnitude and they do not cancel out each other. Thus we can say that the force is unbalanced along the bead. Also the resultant force is found out by adding the forces along with their components.