Question

Resolve the vector A = \[{{A}_{x}}i+{{A}_{y}}j\]along the perpendicular to the line which make angle 60 with x- axis.

Answer 1

Hint: Firstly explaining the vector and some important information related to it. Using line and angle we can find its vector component of the given vector. After it, the perpendicular vector component value can be derived from previous vector angles as the lines are intersecting lines.

Complete step-by-step solution:
Vector is a quantity that has magnitude and direction as both. It is typically represented by an arrow. Vector quantities that have magnitude and direction are as ex: displacement, velocity and acceleration. Other quantities which don’t have direction are called scalars. A vector has magnitude and direction but it doesn’t have position. As long as its length is not changed the vector is not changed too.
In history, vectors were first introduced in geometry and physics before the formalization of the concept of vector space. When one often talks about vectors without stating the vector space to which they belong.
There are some other rules of vector manipulation like subtraction, multiplication by scalar or vector multiplication, and differentiation.
Given:

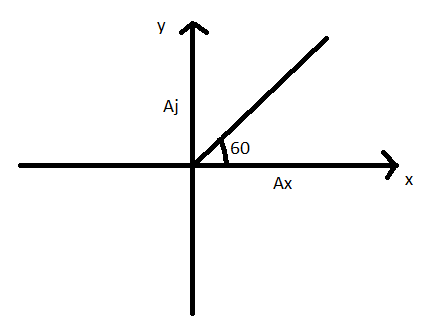
In a two-dimensional coordinate system, any vector can be broken into x-axis and y-axis.as given in the above figure
Line angle \[{{60}^{\circ }}\] with x-axis and x-axis with y-axis make angle \[{{90}^{\circ }}\] then y-axis angle will make \[{{30}^{\circ }}\]. So on other side it’s opposite and below x-axis it will be angle \[{{30}^{\circ }}\]
For example: If we take A vector and line R which makes an angle of θ then
  \[\overset{\scriptscriptstyle\rightharpoonup}{A}=R\cos \theta \]

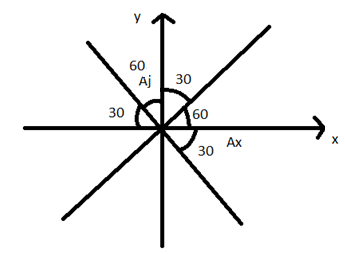
In the above figure, the components can be quickly read. The vector in the component form is A
The trigonometric ratio between magnitude of the vector and component of vector:
\[\cos \theta =\dfrac{adjacent..side}{hypotenuse}\]
Given vector A with angle of 60 and line as \[{{A}_{x}}i\]
Component of A along the line
_{\[\overset{\scriptscriptstyle\rightharpoonup}{A}=\]\[{{A}_{x}}\cos {{60}^{\circ }}+{{A}_{y}}\cos {{30}^{\circ }}\]}
=\[\dfrac{{{A}_{x}}}{2}+{{A}_{y}}\dfrac{\sqrt{3}}{2}\]
Component of A perpendicular to the line
_{\[\overset{\scriptscriptstyle\rightharpoonup}{A}=\]\[{{A}_{x}}\cos {{30}^{\circ }}+{{A}_{y}}\cos {{60}^{\circ }}\]}
=\[{{A}_{x}}\dfrac{\sqrt{3}}{2}+\dfrac{{{A}_{y}}}{2}\]
_{Thus, the final result is A}
=\[{{A}_{x}}\dfrac{\sqrt{3}}{2}+\dfrac{{{A}_{y}}}{2}\]

Note:Vectors have many real-life applications, including situations involving force or velocity. For example, consider the forces acting on a boat crossing a river. The boat's motor generates a force in one direction, and the current of the river generates a force in another direction. Both forces are vectors.