Question

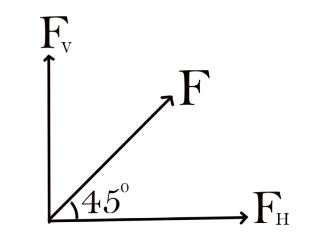
Resolve horizontally and vertically a force $F = 8N$ which makes an angle of ${45^0}$ with the horizontal.

Answer 1

Hint: Any vector in a plane can be resolved in two components. Use the concept of resolution of vectors to find the horizontal and vertical component of the force $F$ given in the question.

Complete step by step answer:
We know that, Any vector in a plane can be resolved in two components. We call the two components as horizontal components and vertical components.
Let the vector make an angle $\theta $ with the horizontal.

Then, the horizontal component of the vector is given by the cosine of the angle of the vector. Vertical component is given by the sin of the angle of the vector.
Let ${F_H}$ be the horizontal component of the force and ${F_V}$ be the vertical component of the force.
${F_H} = F\cos \theta $, As we know the value of Force $F$ is given as $8N$ and angle of this force with horizontal is $45^\circ $.
So we can write the horizontal component of this force using the resolution of the vector concept as.
${F_H} = 8\cos {45^0}$
${F_H} = \dfrac{8}{{\sqrt 2 }}N$ will be the horizontal component of this force
Similarly, we can also write the vertical component of this force as
${F_V} = F\sin \theta $
${F_V} = 8\sin {45^0}$
${F_V} = \dfrac{8}{{\sqrt 2 }}N$

Additional information:
Resolution of Forces is the method in which the process of breaking a force into the two components, basically horizontal and vertical components. On the other hand, also we can say that the process of substituting a force by its components so that the net effect on the body remains the same is called resolution of a force.

Note: This law is not new but can be derived easily with the help of trigonometry. Let us see the proof of this law.
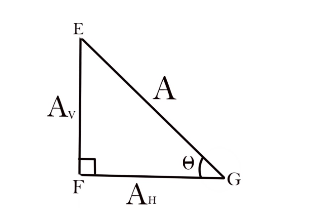
Let a right angle triangle EFG with $\angle F = {90^0}$and $\angle G = \theta $

Now, with respect to $\angle G$,
Perpendicular is the vertical component and base of the triangle is the horizontal triangle as shown in the figure.
Let the length of hypotenuse be $A$, base be ${A_H}$and perpendicular be ${A_V}$.
Now,
$\sin \theta = \dfrac{{{A_V}}}{A}$
$A\sin \theta = {A_V}$ is the vertical component of A
Similarly,
$\cos \theta = \dfrac{{{A_H}}}{A}$
$A\cos \theta = {A_H}$ is the horizontal component of A