Represent the given irrational numbers $\sqrt{3.5},\sqrt{9.4},\sqrt{10.5}$ on the real number line.
Answer
Verified584.7k+ views
Hint: Suppose we have to represent $\sqrt{x}$ on the number line, then we will draw it by following a few steps, which are as follows. First we will draw a line of x units and produce it as (x + 1) units. We will then find the midpoint of (x + 1) and then from the end point of x, we will draw a perpendicular touching the semi-circle formed by taking (x + 1) diameter. This perpendicular line will give us $\sqrt{x}$.
Complete step-by-step solution -
It is given in the question that we have to represent $\sqrt{3.5},\sqrt{9.4},\sqrt{10.5}$ on the real number line.
Now, we will represent $\sqrt{3.5}$ on the number line, so we have to follow a few steps which are shown below.
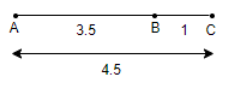
Step 1: We will draw a line segment AB of 3.5 units.
Step 2: We will produce 3.5 by 1 unit and name the end point as C. So, we get,
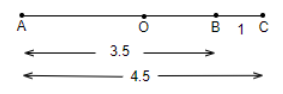
Step 3: We will find the midpoint of AC and name the mid-point as O.
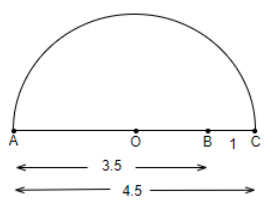
Step 4: We will draw a semicircle from O taking OA as the radius, so we get,
Step 5: We will draw a perpendicular line from point B touching the semicircle at point D.
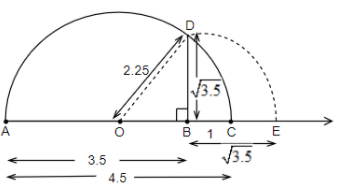
Step 6: We will get BD is equal to $\sqrt{3.5}$ from the calculation below. Then, to represent it in the number line we will draw an arc with point B as the center and BD as the radius to the line and will mark that point as E. So BE will represent $\sqrt{3.5}$ in the number line.
In triangle OBD, we will apply the Pythagoras theorem, so we get,
$B{{D}^{2}}=O{{D}^{2}}-O{{B}^{2}}$
Now, we know that OD = OC, also we can write OB as OC – BC, so we can write,
$B{{D}^{2}}=O{{C}^{2}}-{{\left( OC-BC \right)}^{2}}$
We know that ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$, so we can write,
$\begin{align}
& B{{D}^{2}}=O{{C}^{2}}-\left( O{{C}^{2}}+B{{C}^{2}}-2\left( OC \right)\left( BC \right) \right) \\
& B{{D}^{2}}=O{{C}^{2}}-O{{C}^{2}}-B{{C}^{2}}+2\left( OC \right)\left( BC \right) \\
& B{{D}^{2}}=2\left( OC \right)\left( BC \right)-B{{C}^{2}} \\
\end{align}$
Now, from the figure, we can see that O is the midpoint of AC, so we get OC as half of AC, that is, $OC=\dfrac{4.5}{2}=2.25$.
Therefore, on putting the values of OC as 2.25 and BC as 1, we get,
$\begin{align}
& B{{D}^{2}}=2\times 2.25\times 1-1 \\
& B{{D}^{2}}=4.5-1=3.5 \\
& BD=\sqrt{3.5} \\
\end{align}$
Thus, we get $BD=\sqrt{3.5}$.
Now, we will represent $\sqrt{9.4}$ on the number line and we will follow the following steps.
Step 1: We will draw a line segment AB of 9.4 units.
Step 2: We will produce 9.4 by 1 unit and mark the end point as C. So, we get,
Step 3: We will find the midpoint of AC and name the mid-point as O.
Step 4: We will draw a semicircle from O taking OA as the radius, so we get,
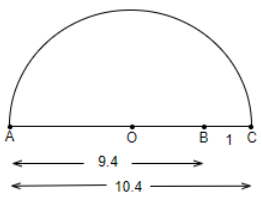
Step 5: We will draw a perpendicular line from point B touching the semicircle at point D.
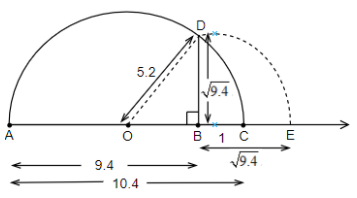
Step 6: We will get BD is equal to $\sqrt{9.4}$ from the calculation below. Then, to represent it in the number line we will draw an arc with point B as the center and BD as the radius to the line and will mark that point as E. So BE will represent $\sqrt{9.4}$ in the number line.
In triangle OBD, we will apply the Pythagoras theorem, so we get,
$B{{D}^{2}}=O{{D}^{2}}-O{{B}^{2}}$
Now, we know that OD = OC, also we can write OB as OC – BC, so we can write,
$B{{D}^{2}}=O{{C}^{2}}-{{\left( OC-BC \right)}^{2}}$
We know that ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$, so we can write,
$\begin{align}
& B{{D}^{2}}=O{{C}^{2}}-\left( O{{C}^{2}}+B{{C}^{2}}-2\left( OC \right)\left( BC \right) \right) \\
& B{{D}^{2}}=O{{C}^{2}}-O{{C}^{2}}-B{{C}^{2}}+2\left( OC \right)\left( BC \right) \\
& B{{D}^{2}}=2\left( OC \right)\left( BC \right)-B{{C}^{2}} \\
\end{align}$
Now, from the figure, we can see that O is the midpoint of AC, so we get OC as half of AC, that is, $OC=\dfrac{10.4}{2}=5.2$.
Therefore, on putting the values of OC as 5.2 and BC as 1, we get,
$\begin{align}
& B{{D}^{2}}=2\times 5.2\times 1-1 \\
& B{{D}^{2}}=10.4-1=9.4 \\
& BD=\sqrt{9.4} \\
\end{align}$
Thus, we get $BD=\sqrt{9.4}$.
Now, we will represent $\sqrt{10.5}$ on the number line and we will follow the following steps.
Step 1: We will draw a line segment AB of 10.5 units.
Step 2: We will produce 10.5 by 1 unit and mark the end point as C. So, we get,
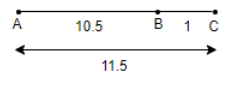
Step 3: We will find the midpoint of AC and name the mid-point as O.
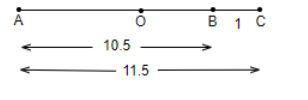
Step 4: We will draw a semicircle from O taking OA as the radius, so we get,
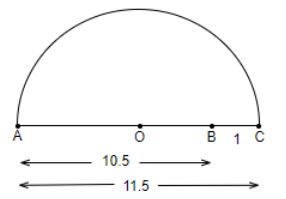
Step 5: We will draw a perpendicular line from point B touching the semicircle at point D.
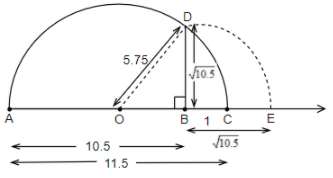
Step 6: We will get BD is equal to $\sqrt{10.5}$ from the calculation below. Then, to represent it in the number line we will draw an arc with point B as the center and BD as the radius to the line and will mark that point as E. So BE will represent $\sqrt{10.5}$ in the number line.
In triangle OBD, we will apply the Pythagoras theorem, so we get,
$B{{D}^{2}}=O{{D}^{2}}-O{{B}^{2}}$
Now, we know that OD = OC, also we can write OB as OC – BC, so we can write,
$B{{D}^{2}}=O{{C}^{2}}-{{\left( OC-BC \right)}^{2}}$
We know that ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$, so we can write,
$\begin{align}
& B{{D}^{2}}=O{{C}^{2}}-\left( O{{C}^{2}}+B{{C}^{2}}-2\left( OC \right)\left( BC \right) \right) \\
& B{{D}^{2}}=O{{C}^{2}}-O{{C}^{2}}-B{{C}^{2}}+2\left( OC \right)\left( BC \right) \\
& B{{D}^{2}}=2\left( OC \right)\left( BC \right)-B{{C}^{2}} \\
\end{align}$
Now, from the figure, we can see that O is the midpoint of AC, so we get OC as half of AC, that is, $OC=\dfrac{11.5}{2}=5.75$.
Therefore, on putting the values of OC as 5.75 and BC as 1, we get,
$\begin{align}
& B{{D}^{2}}=2\times 5.75\times 1-1 \\
& B{{D}^{2}}=11.5-1=10.5 \\
& BD=\sqrt{10.5} \\
\end{align}$
Thus, we get $BD=\sqrt{10.5}$.
Note: Many students tend to find the roots of $\sqrt{3.5},\sqrt{9.4},\sqrt{10.5}$ and then represent it on the number line which is not recommended. As doing it is very tough and there are chances of errors while doing so. So it is better to follow the construction method as done in this question.
Complete step-by-step solution -
It is given in the question that we have to represent $\sqrt{3.5},\sqrt{9.4},\sqrt{10.5}$ on the real number line.
Now, we will represent $\sqrt{3.5}$ on the number line, so we have to follow a few steps which are shown below.
Step 1: We will draw a line segment AB of 3.5 units.
Step 2: We will produce 3.5 by 1 unit and name the end point as C. So, we get,
Step 3: We will find the midpoint of AC and name the mid-point as O.
Step 4: We will draw a semicircle from O taking OA as the radius, so we get,
Step 5: We will draw a perpendicular line from point B touching the semicircle at point D.
Step 6: We will get BD is equal to $\sqrt{3.5}$ from the calculation below. Then, to represent it in the number line we will draw an arc with point B as the center and BD as the radius to the line and will mark that point as E. So BE will represent $\sqrt{3.5}$ in the number line.
In triangle OBD, we will apply the Pythagoras theorem, so we get,
$B{{D}^{2}}=O{{D}^{2}}-O{{B}^{2}}$
Now, we know that OD = OC, also we can write OB as OC – BC, so we can write,
$B{{D}^{2}}=O{{C}^{2}}-{{\left( OC-BC \right)}^{2}}$
We know that ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$, so we can write,
$\begin{align}
& B{{D}^{2}}=O{{C}^{2}}-\left( O{{C}^{2}}+B{{C}^{2}}-2\left( OC \right)\left( BC \right) \right) \\
& B{{D}^{2}}=O{{C}^{2}}-O{{C}^{2}}-B{{C}^{2}}+2\left( OC \right)\left( BC \right) \\
& B{{D}^{2}}=2\left( OC \right)\left( BC \right)-B{{C}^{2}} \\
\end{align}$
Now, from the figure, we can see that O is the midpoint of AC, so we get OC as half of AC, that is, $OC=\dfrac{4.5}{2}=2.25$.
Therefore, on putting the values of OC as 2.25 and BC as 1, we get,
$\begin{align}
& B{{D}^{2}}=2\times 2.25\times 1-1 \\
& B{{D}^{2}}=4.5-1=3.5 \\
& BD=\sqrt{3.5} \\
\end{align}$
Thus, we get $BD=\sqrt{3.5}$.
Now, we will represent $\sqrt{9.4}$ on the number line and we will follow the following steps.
Step 1: We will draw a line segment AB of 9.4 units.
Step 2: We will produce 9.4 by 1 unit and mark the end point as C. So, we get,
Step 3: We will find the midpoint of AC and name the mid-point as O.
Step 4: We will draw a semicircle from O taking OA as the radius, so we get,
Step 5: We will draw a perpendicular line from point B touching the semicircle at point D.
Step 6: We will get BD is equal to $\sqrt{9.4}$ from the calculation below. Then, to represent it in the number line we will draw an arc with point B as the center and BD as the radius to the line and will mark that point as E. So BE will represent $\sqrt{9.4}$ in the number line.
In triangle OBD, we will apply the Pythagoras theorem, so we get,
$B{{D}^{2}}=O{{D}^{2}}-O{{B}^{2}}$
Now, we know that OD = OC, also we can write OB as OC – BC, so we can write,
$B{{D}^{2}}=O{{C}^{2}}-{{\left( OC-BC \right)}^{2}}$
We know that ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$, so we can write,
$\begin{align}
& B{{D}^{2}}=O{{C}^{2}}-\left( O{{C}^{2}}+B{{C}^{2}}-2\left( OC \right)\left( BC \right) \right) \\
& B{{D}^{2}}=O{{C}^{2}}-O{{C}^{2}}-B{{C}^{2}}+2\left( OC \right)\left( BC \right) \\
& B{{D}^{2}}=2\left( OC \right)\left( BC \right)-B{{C}^{2}} \\
\end{align}$
Now, from the figure, we can see that O is the midpoint of AC, so we get OC as half of AC, that is, $OC=\dfrac{10.4}{2}=5.2$.
Therefore, on putting the values of OC as 5.2 and BC as 1, we get,
$\begin{align}
& B{{D}^{2}}=2\times 5.2\times 1-1 \\
& B{{D}^{2}}=10.4-1=9.4 \\
& BD=\sqrt{9.4} \\
\end{align}$
Thus, we get $BD=\sqrt{9.4}$.
Now, we will represent $\sqrt{10.5}$ on the number line and we will follow the following steps.
Step 1: We will draw a line segment AB of 10.5 units.
Step 2: We will produce 10.5 by 1 unit and mark the end point as C. So, we get,
Step 3: We will find the midpoint of AC and name the mid-point as O.
Step 4: We will draw a semicircle from O taking OA as the radius, so we get,
Step 5: We will draw a perpendicular line from point B touching the semicircle at point D.
Step 6: We will get BD is equal to $\sqrt{10.5}$ from the calculation below. Then, to represent it in the number line we will draw an arc with point B as the center and BD as the radius to the line and will mark that point as E. So BE will represent $\sqrt{10.5}$ in the number line.
In triangle OBD, we will apply the Pythagoras theorem, so we get,
$B{{D}^{2}}=O{{D}^{2}}-O{{B}^{2}}$
Now, we know that OD = OC, also we can write OB as OC – BC, so we can write,
$B{{D}^{2}}=O{{C}^{2}}-{{\left( OC-BC \right)}^{2}}$
We know that ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$, so we can write,
$\begin{align}
& B{{D}^{2}}=O{{C}^{2}}-\left( O{{C}^{2}}+B{{C}^{2}}-2\left( OC \right)\left( BC \right) \right) \\
& B{{D}^{2}}=O{{C}^{2}}-O{{C}^{2}}-B{{C}^{2}}+2\left( OC \right)\left( BC \right) \\
& B{{D}^{2}}=2\left( OC \right)\left( BC \right)-B{{C}^{2}} \\
\end{align}$
Now, from the figure, we can see that O is the midpoint of AC, so we get OC as half of AC, that is, $OC=\dfrac{11.5}{2}=5.75$.
Therefore, on putting the values of OC as 5.75 and BC as 1, we get,
$\begin{align}
& B{{D}^{2}}=2\times 5.75\times 1-1 \\
& B{{D}^{2}}=11.5-1=10.5 \\
& BD=\sqrt{10.5} \\
\end{align}$
Thus, we get $BD=\sqrt{10.5}$.
Note: Many students tend to find the roots of $\sqrt{3.5},\sqrt{9.4},\sqrt{10.5}$ and then represent it on the number line which is not recommended. As doing it is very tough and there are chances of errors while doing so. So it is better to follow the construction method as done in this question.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success
Master Class 9 English: Engaging Questions & Answers for Success
Master Class 9 Science: Engaging Questions & Answers for Success
Class 9 Question and Answer - Your Ultimate Solutions Guide
Master Class 12 Economics: Engaging Questions & Answers for Success
Master Class 12 Maths: Engaging Questions & Answers for Success
Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE
Write the 6 fundamental rights of India and explain in detail
Difference Between Plant Cell and Animal Cell
What is pollution? How many types of pollution? Define it
What is the Full Form of ISI and RAW