Question

Represent the following on the number-line
(A) \[\sqrt{10}\]
(B) \[\sqrt{13}\]
(C) \[\sqrt{2}\]

Answer 1

Hint: First of all, take the length of the perpendicular BA as 1 unit and the length of the base OA as 3 units. Now, use the Pythagoras theorem for the \[\Delta BAO\] . According to the Pythagoras theorem we have, \[Hypotenuse=\sqrt{{{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}}\] . Now, calculate the length of the hypotenuse. Then, by taking OB as the radius and O as the center, draw an arc intersecting the x-axis at point C. Now, the number \[\sqrt{10}\] is represented by the length of the line OC. Similarly, to represent \[\sqrt{13}\] , take the length of the perpendicular BA as 1 unit and the length of the base OA as 3 units. Similarly, to represent \[\sqrt{2}\] , take the length of the perpendicular BA as 1 unit and the length of the base OA as 1 unit. Similarly, to represent \[\sqrt{5}\] , take the length of the perpendicular BA as 1 unit and the length of the base OA as 2 units. Similarly, to represent \[\sqrt{3}\] , take the length of the perpendicular BA as 1 unit and the length of the base OA as \[\sqrt{2}=1.414\] units.

Complete step-by-step answer:
According to the question, we are given some numbers and we have to represent those numbers on the number line.
First of all, let us take \[\sqrt{10}\] and represent it on the number line.
To represent the number \[\sqrt{10}\] , we require the Pythagoras theorem.
According to the Pythagoras theorem, we know that
\[Hypotenuse=\sqrt{{{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}}\] …………………………………………..(1)
We have to take the measure of the hypotenuse equal to \[\sqrt{10}\] units.
Now, taking 3 units as the base OA on the x-axis and a perpendicular BA of length 1 unit on that base.

Plotting OA = 3 units on the number line and the perpendicular BA = 1 unit, we get

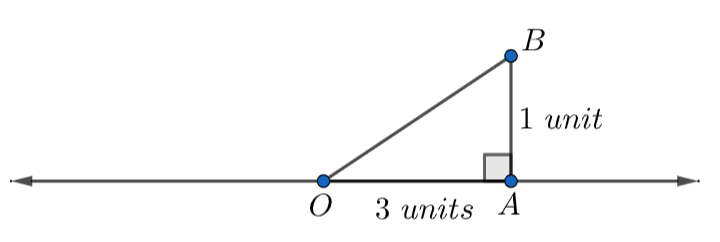
In the \[\Delta BAO\] , we have
Perpendicular = BA = 1 unit …………………………………….(2)
Base = OA = 3 units ……………………………………….(3)
From equation (1), we have \[Hypotenuse=\sqrt{{{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}}\] .
From equation (2) and equation (3), we have the lengths of the base and the perpendicular.
On putting, Perpendicular = BA = 1 unit and Base = OA = 3 units in equation (1), we get
\[\begin{align}
  & \Rightarrow OB=\sqrt{{{\left( 1 \right)}^{2}}+{{\left( 3 \right)}^{2}}} \\
 & \Rightarrow OB=\sqrt{1+9} \\
 & \Rightarrow OB=\sqrt{10} \\
\end{align}\]
Now, take OB as a radius and draw an arc intersecting the real axis that is our x-axis at C.
Since \[\overset\frown{BC}\] is an arc that is drawn by taking O as the center, we can say that the lengths OB and OC are equal because all the radius of an arc are equal to each other.

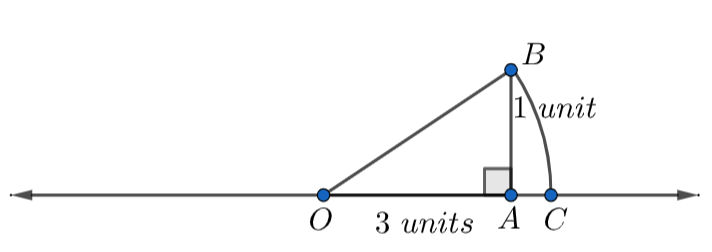
Therefore, \[OB=OC=\sqrt{10}\] .
Here, OC represents the number \[\sqrt{10}\] on the real number line.
To represent \[\sqrt{13}\] on the real number line, we have to repeat the same procedure.
Let us take OA=3 units on the x-axis and BA=2 units which is also perpendicular to OA.

Now, plotting OA = 3 units on the number line and the perpendicular BA = 1 unit, we get

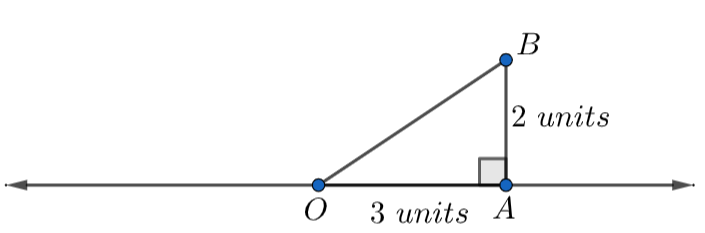
In the \[\Delta BAO\] , we have
Perpendicular = BA = 2 unit …………………………………….(4)
Base = OA = 3 units ……………………………………….(5)
Similarly, putting Perpendicular = BA = 2 units and Base = OA = 3 units in equation (1), we get
\[\begin{align}
  & \Rightarrow OB=\sqrt{{{\left( 3 \right)}^{2}}+{{\left( 2 \right)}^{2}}} \\
 & \Rightarrow OB=\sqrt{9+4} \\
 & \Rightarrow OB=\sqrt{13} \\
\end{align}\]
Now, take OB as a radius and draw an arc intersecting the real axis that is our x-axis at C.
Since \[\overset\frown{BC}\] is an arc that is drawn by taking O as the center, we can say that the lengths OB and OC are equal because all the radius of an arc are equal to each other.

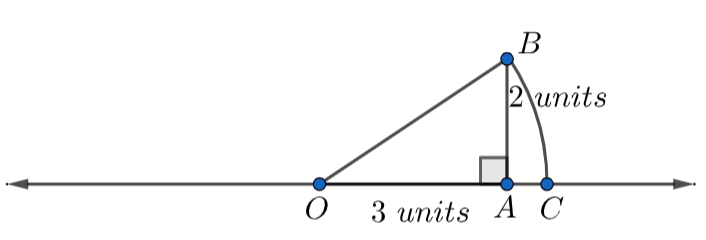
Therefore, \[OB=OC=\sqrt{13}\] .
Here, OC represents the number \[\sqrt{13}\] on the real number line.
To represent \[\sqrt{2}\] on the real number line, we have to repeat the same procedure again.
Let us draw OA=1 unit on the x-axis and BA=1 unit which is also perpendicular to OA.

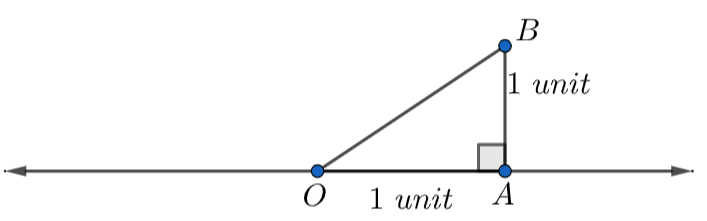
In the \[\Delta BAO\] , we have
Perpendicular = BA = 1 unit …………………………………….(6)
Base = OA = 1 unit ……………………………………….(7)
Similarly, putting Perpendicular = BA = 1 unit and Base = OA = 1 unit in equation (1), we get
\[\begin{align}
  & \Rightarrow OB=\sqrt{{{\left( 1 \right)}^{2}}+{{\left( 1 \right)}^{2}}} \\
 & \Rightarrow OB=\sqrt{1+1} \\
 & \Rightarrow OB=\sqrt{2} \\
\end{align}\]
Now, take OB as a radius and draw an arc intersecting the real axis that is our x-axis at C.
Since \[\overset\frown{BC}\] is an arc that is drawn by taking O as the center, we can say that the lengths OB and OC are equal because all the radius of an arc are equal to each other.

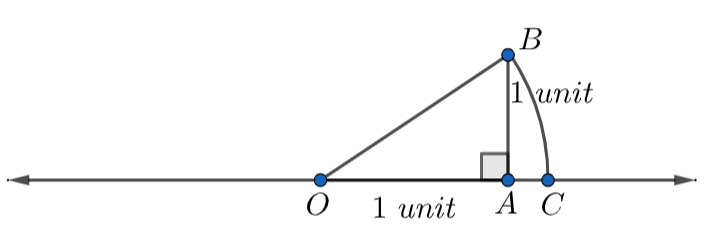
Therefore, \[OB=OC=\sqrt{2}\] .
Here, OC represents the number \[\sqrt{2}\] on the real number line.

Note: Whenever this type question appears, always approach it by using the Pythagoras theorem and assume a suitable value of base and perpendicular. For instance, \[\sqrt{10}=3.16\] . So, here take the base equal to 3 and then calculate the perpendicular so that the hypotenuse is equal to \[\sqrt{10}\] .