Question

Represent $\sqrt{7}$ on the number line.

Answer 1

Hint: Use the fact that if two sides of a right-angled triangle are $\sqrt{x}$ and 1, then the hypotenuse is given by $\sqrt{x+1}$. Hence form a right-angled triangle with sides, 1 and 1. The hypotenuse will be $\sqrt{2}$. Then using the length of hypotenuse form another right-angled triangle with sides, $\sqrt{3}$ and 1. The hypotenuse of that triangle will be $\sqrt{3}$. Continue in the same way till we get the hypotenuse length as $\sqrt{7}$. Now extend compass length to be equal to $\sqrt{7}$ (Keep one arm of the compass on one endpoint of the hypotenuse and the other arm on the other endpoint of the hypotenuse). Draw an arc with 0 as the centre and let it intersect the positive x-axis at some point. The point then represents $\sqrt{7}$ on the number line.

Complete step-by-step answer:
Consider a right-angled triangle with side length as 1,1 as shown below

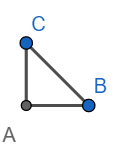
Hence $BC=\sqrt{1^2+1^2}=\sqrt{2}$
Draw CD perpendicular BC and CD = 1 unit as shown below.

Hence $BD=\sqrt{{\left(\sqrt{2}\right)}^2+1^2}=\sqrt{3}$
Draw CE perpendicular to BD, CE = 1 unit.

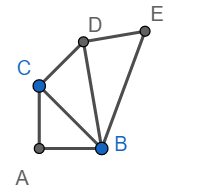
Hence $BE=\sqrt{{\left(\sqrt{3}\right)}^2+1}=\sqrt{4}$
Draw EF perpendicular to BE, EF = 1 unit as shown below

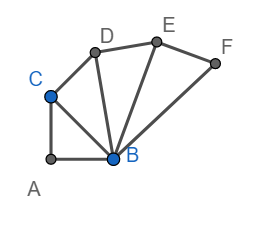
Hence $BF=\sqrt{{\left(\sqrt{4}\right)}^2+1}=\sqrt{5}$
Draw FG perpendicular BF and FG = 1 unit as shown below.

Hence $BG=\sqrt{{\left(\sqrt{5}\right)}^2+1}=\sqrt{6}$
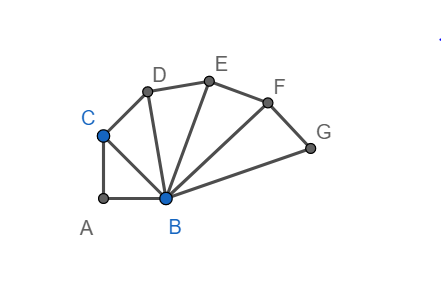
Draw GH perpendicular BG and GH = 1 unit, as shown below.

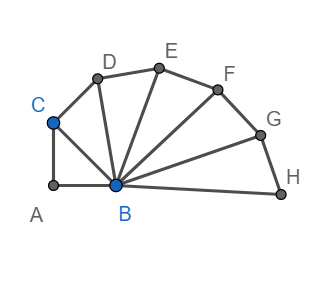
Hence $BH=\sqrt{{\left(\sqrt{6}\right)}^2+1}=\sqrt{7}$
With O as centre and radius BH, mark draw an arc and let it intersect the positive x-axis at M. M represents $\sqrt{7}$ on the number line.

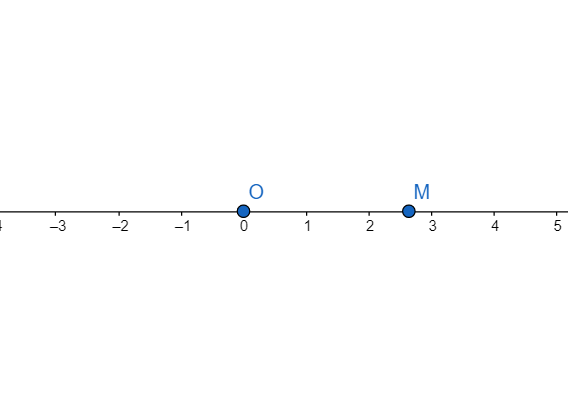
Hence $\sqrt{7}$ is represented on the number line.

Note: Alternative method: Best Method:
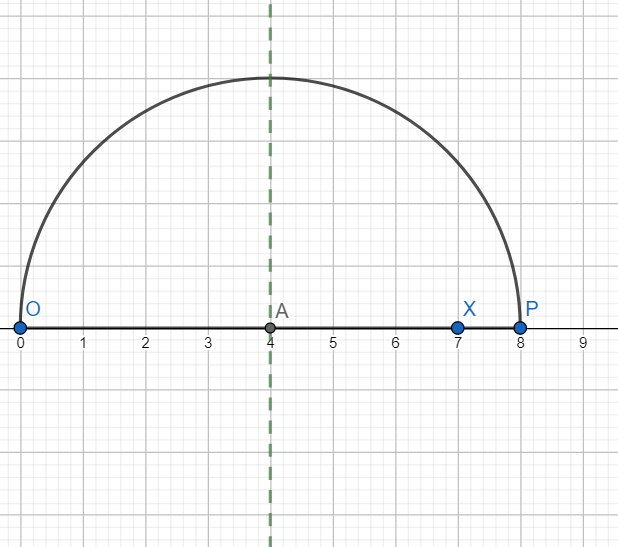
Draw OX = 7 units.
Extend OX to P such that XP = 1 unit.

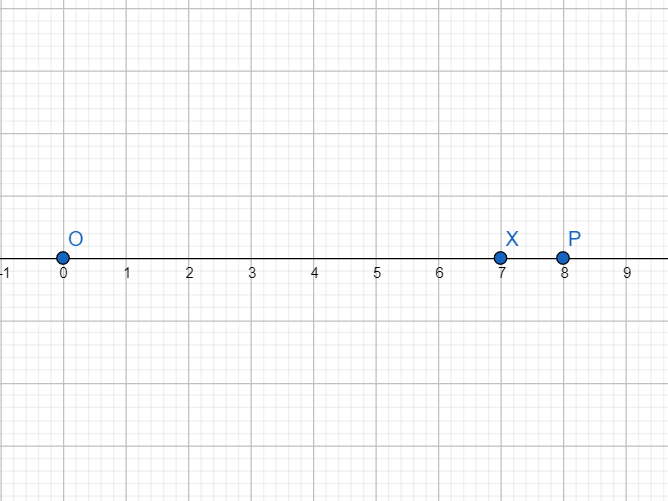
Now locate the midpoint of OP by drawing perpendicular bisector of OP. Let it intersect OP at A as shown below.

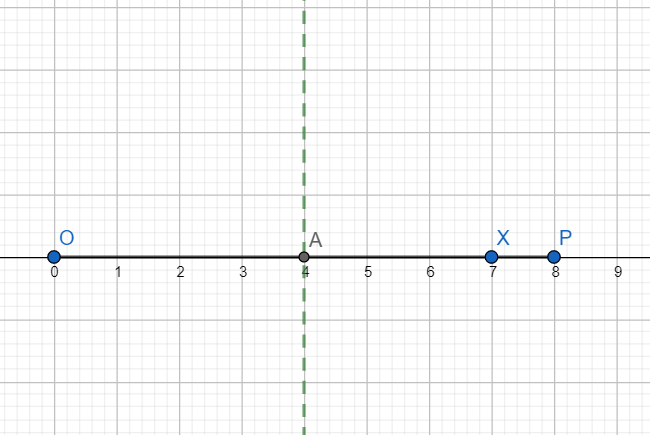
With A as centre and radius OP draw a semicircle as shown below

Now draw a line parallel to the perpendicular bisector through X and let it intersect the semicircle at B as shown below.

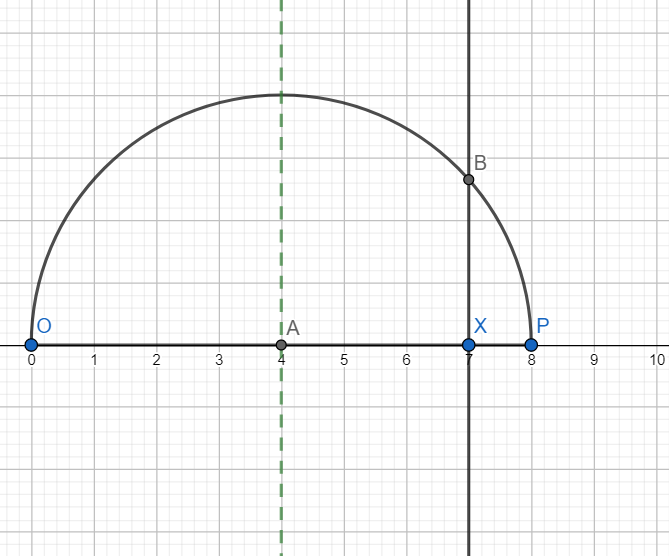
Hence $XB=\sqrt{7}$
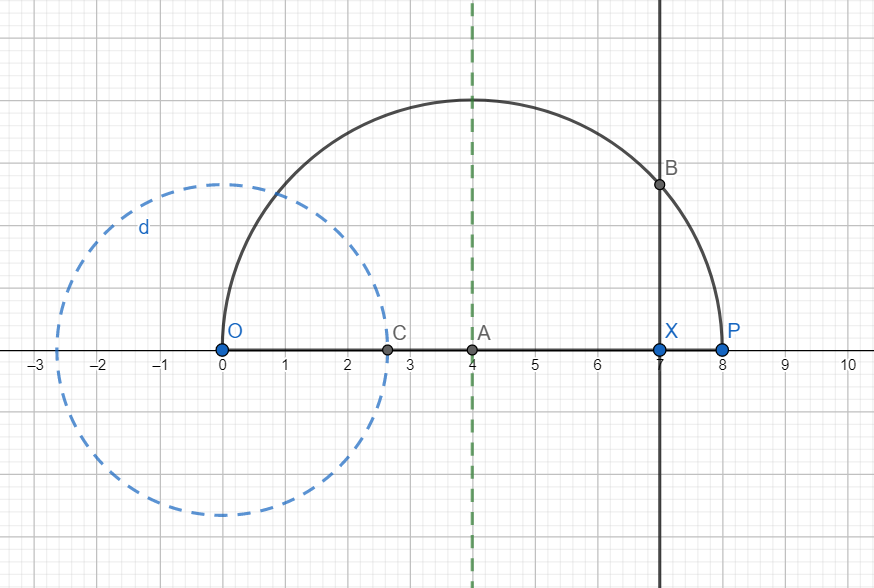
Now extend compass to be of radius XB draw an arc from O and let it intersect OP at C.
C represents $\sqrt{7}$ on the number line.