Question

Represent $\sqrt{5}$ on the number line.

Answer 1

Hint:Use the Pythagoras theorem to represent $\sqrt{5}$ on the number line. It is given as
${{\left( \text{hypotenuse} \right)}^{\text{2}}}\text{ = }{{\left( \text{Base} \right)}^{\text{2}}}\text{ + }{{\left( \text{Perpendicular} \right)}^{\text{2}}}$
Split $\sqrt{5}\to {{\left( \sqrt{5} \right)}^{2}}={{\left( 2 \right)}^{2}}+{{\left( 1 \right)}^{2}}$
Get a point at a distance of 2 units in the right direction of 0 and draw perpendicularly at that point to the number line of 1 unit length. Join 0 and the extreme end of the perpendicular of 1 unit, this distance will be $\sqrt{5}$. Take 0 as a centre and draw an arc of length $\sqrt{5}$ intersecting the number line.

Complete step-by-step answer:
As, we know $\sqrt{5}$ s an irrational number, so, we cannot convert $\sqrt{5}\to \dfrac{p}{q}$ form and cannot be able to represent $\sqrt{5}$ directly to the number line. So, let us relate with another approach of representation.
As we know the Pythagoras theorem for a right angled triangle is given as
 ${{\left( \text{hypotenuse} \right)}^{\text{2}}}\text{ = }{{\left( \text{Base} \right)}^{\text{2}}}\text{ + }{{\left( \text{Perpendicular} \right)}^{\text{2}}}$………..(i)

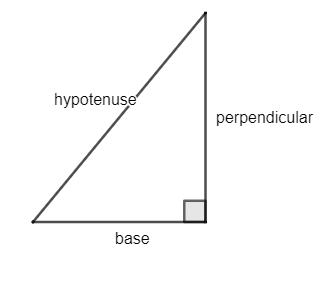
So, take the length of base as ‘2’ and the perpendicular as ‘1’. So, we get from equation (i) as
$\begin{align}
  & {{\left( \text{hypotenuse} \right)}^{\text{2}}}\text{ = }{{\left( \text{2} \right)}^{\text{2}}}\text{ + }{{\left( \text{1} \right)}^{\text{2}}}=5 \\
 & {{\left( \text{hypotenuse} \right)}^{\text{2}}}\text{ = }\sqrt{5} \\
\end{align}$
It means
${{\left( \sqrt{5} \right)}^{2}}={{\left( 1 \right)}^{2}}+{{\left( 2 \right)}^{2}}$……………(ii)
Now, a number line can be drawn as

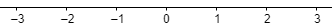
Now, let us suppose a point A from 2 units from ‘0’ in the right direction.
So, represent point ‘0’ as P and 2 as A. so, we get

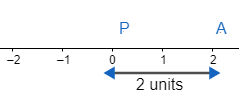
Let us draw a line making ${{90}^{\circ }}$ to the line segment PA at point A i.e. a perpendicular at point A on line segment PA. so, we get the above diagram as

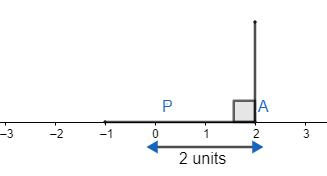
Now, put an arc on the perpendicular at point A in the upward direction at the distance of 1 unit. So, we get diagram as

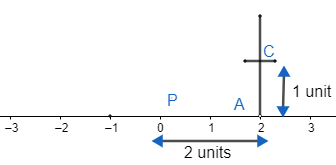
Now, suppose the point at 1 unit distance from A is ‘C’. and join the points P and C to get the line segment PC. So, we get diagram as

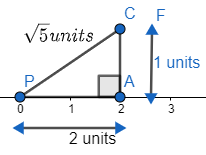
Where, length PC will be of $\sqrt{\text{5}}\text{ units }\to \text{ }\!\!\Delta\!\!\text{ APC}$ is a right angle triangle and ${{2}^{2}}+{{1}^{2}}={{\left( \sqrt{5} \right)}^{2}}$ from equation (ii). Now, take PC as a radius and P as a centre and draw an arc intersecting the number line, with the help of compass (or we can draw a circle of radius $PC=\sqrt{5}$ and centre as P, as well).
So, we get the diagram as

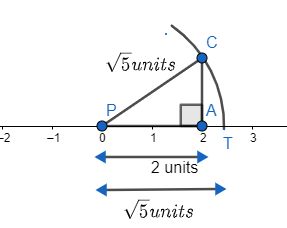
As, PC is taken as a radius of the circle with circle at P. It means the length PC should be equal to PT as well, as both are representing the radius of the same circle and the radius is the same everywhere for the same circle. So, let T be the point of intersection of a circle on the number line.
Hence, point is the point representing $\sqrt{5}$ on the number line as length PT = $\sqrt{5}$ units.So, T is the required point for representing $\sqrt{5}$ units.

Note: One may split $(\sqrt{5})^{2}\to {{\left( \sqrt{3} \right)}^{2}}+{{\left( \sqrt{2} \right)}^{2}}$ as well. And with this approach, we need to represent $\sqrt{3},\sqrt{2}$ separately, then, we need to represent $\sqrt{5}$.$(\sqrt{3})^{2}$ can be written as ${{\left( \sqrt{2} \right)}^{2}}+{{\left( 1 \right)}^{2}},{{\left( \sqrt{2} \right)}^{2}}\to {{1}^{2}}+{{1}^{2}}$. So, the approach will not be flexible than given in the solution. One may try to calculate $\sqrt{5}$ in decimal form and hence, try to represent it in the decimal form. But it is not possible to represent $\sqrt{5}$ on a number line by representing it in decimal form. As $\sqrt{5}$ is non-terminating and non-repeating decimal, so, we will not be able to represent it in decimal form on the number line.