Question

Represent $\dfrac{8}{5}$ and $-\dfrac{8}{5}$ on the number line.

Answer 1

Hint: We must first convert these improper fractions into mixed fraction form. We know that we can represent $\dfrac{8}{5}$ as $1\dfrac{3}{5}$ and $-\dfrac{8}{5}$ as $-1\dfrac{3}{5}$. So, we will need to divide the part between 1 and 2, and -1 and -2 into 5 parts. Then, we can easily plot the points $\dfrac{8}{5}$ and $-\dfrac{8}{5}$ on the number line.

Complete step by step answer:
We know that we can write the improper fraction $\dfrac{8}{5}$ as $1\dfrac{3}{5}$ in the mixed fraction form. Also, we can say that $1\dfrac{3}{5}$ is nothing but $1+\dfrac{3}{5}$. So, to represent $\dfrac{8}{5}$ on the number line, we can plot the point representing $1+\dfrac{3}{5}$.
We know that $\dfrac{3}{5}<1$, and so $1+\dfrac{3}{5}=\dfrac{8}{5}<2$. So let us first plot the points 1 and 2 on the number line.

Now, we need to plot the point $\dfrac{3}{5}$ after the point 1. We know that the fraction $\dfrac{3}{5}$ means 3 parts out of 5. So, let us now divide the distance between 1 and 2 into 5 parts.
For this, we will need to draw a line at point 2 making an acute angle with the number line.

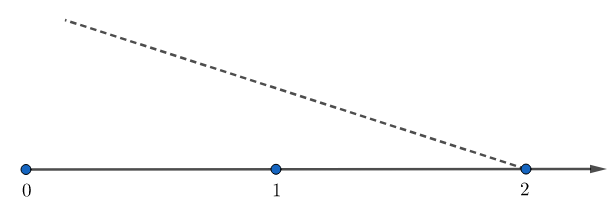
Now, using a compass with 2 as centre and any suitable radius, we will draw an arc intersecting this dotted line at ${{A}_{1}}$, and then with ${{A}_{1}}$ as centre and same radius, we must draw another arc intersecting the same dotted line at ${{A}_{2}}$. Repeating the same process, we must draw 3 more arcs intersecting the dotted line at ${{A}_{3}},{{A}_{4}}\text{ and }{{A}_{5}}$.

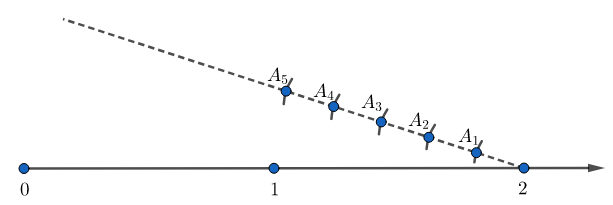
Now, we must join the points 1 and ${{A}_{5}}$. Now, from the point ${{A}_{4}}$, we must draw another line parallel to the previous one and repeat the same process for ${{A}_{3}},{{A}_{2}}\text{ and }{{A}_{1}}$.

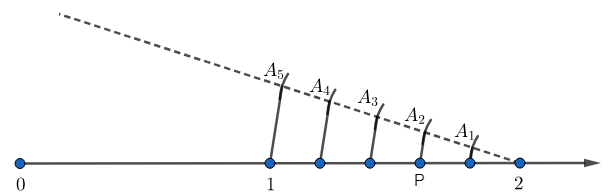
Hence, we have divided the distance between 1 and 2 into 5 parts. The point P represents the 3rd part out of 5, which is $\dfrac{3}{5}$. This point is after 1 and so it represents $1+\dfrac{3}{5}$.
Hence, the point P represents the fraction $\dfrac{8}{5}$.
We can repeat the same process for $-\dfrac{8}{5}$, but on the left side of the origin.

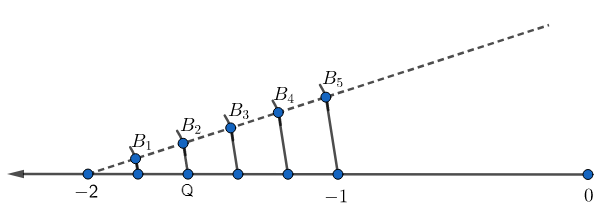
Here, the point Q represents the point $-\dfrac{8}{5}$.

Note: We know that we can use a pair of set squares for drawing parallel lines. We must keep in mind that we cannot represent the improper fractions directly on the number line. We need to convert them into mixed fractions before representing them on the number line.