Question

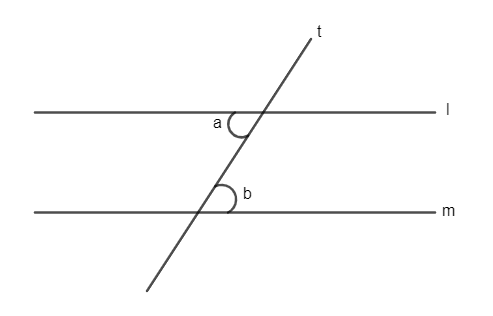
What is the relationship between $\angle a$ and $\angle b$?

Answer 1

Hint: In this question we have been given with a set of lines which are $l,m$ and $t$. We also have two angles $a$ and $b$, and we have to find the relationship between the two given angles. We will first look at the lines $l$ and $m$, and deduce the relationship between them. We will then find out what relationship the line $t$ has with the lines $l$ and $m$. After finding the relationship we can find what the relationship between the angles $a$ and $b$ is and get the required solution.

Complete step by step solution:
We can see from the diagram that the lines $l$ and $m$ are parallel lines. Parallel lines are lines which are at the same plane and lines which will never intersect.
We can see that the line $t$ is a transversal line. A transversal line is a line which passes through a minimum of two lines. We can see that line $t$ passes through the lines $l$ and $m$ therefore, it is a transversal line.
Now when two lines are crossed by a third line called the transversal line. then the angles formed at the intersection points are known as alternate interior angles which have the same value.
Since $\angle a$ and $\angle b$ are alternate interior angles and alternate interior angles are equal to each other, we get $\angle a=\angle b$, which is the required solution.

Note: It is to be remembered that in this question we have the angles $\angle a$ and $\angle b$ in the interior side of the intersection. The angles formed outside the intersection of the angles are called alternate exterior angles. Various other properties such as vertical lines, corresponding angles, consecutive interior angles should also be remembered.