Question

What regular polygons can result when a cube is cut by a plane?

Answer 1

Hint: Here, in the given question, we need to find what regular polygons can result when a cube is cut by a plane. A surface comprising all the straight lines that join any two points lying on it is called a plane in geometry. As we know there are three planes. We will cut the cube one by one in three panes to find our answer.

Complete step by step answer:
Let us first cut the cube by $xy$ plane. The $xy$ plane is the plane that contains the $x - axes$ and $y - axes$.

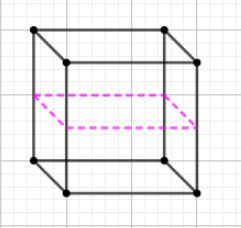
As you can see the cube is now divided into two cuboids. A cuboid is a regular polygon. Now, we will cut the cube by $yz$ plane. The $yz$ plane is the plane that contains the $y - axes$ and $z - axes$.

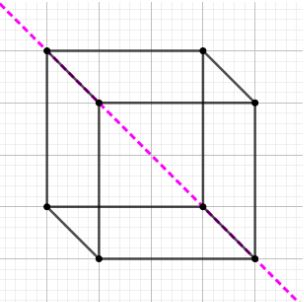
As you can see, the cube is now divided diagonally which results in two prisms. Prism is a regular polygon.Now, we will cut the cube by a $xz$ plane. The $xz$ plane is the plane that contains the $x - axes$ and $z - axes$.

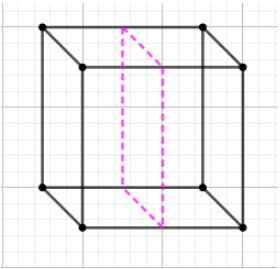
As you can see the cube is now divided into two cuboids. A cuboid is a regular polygon.

Therefore, when we cut a cube by a plane it results in two regular polygons- cuboid and prism.

Note: Remember that to solve this type of question, cut the regular solids in three planes one-by-one. Remember that if we cut a sphere by any plane it will result in two hemispheres. Remember that if we cut a cube into two prisms, the total surface area of two prisms will always remain equal to the total surface area of the cube.