Question

Refractive index of an equilateral prism is $\sqrt{2}$ . Then:
(This question has multiple correct options)
  A. minimum deviation from the prism can be \[30{}^\circ \].
  B. minimum deviation from the prism can be \[45{}^\circ \].
  C. at angle of incidence \[45{}^\circ \], deviation is minimum
  D. at angle of incidence \[60{}^\circ \], deviation is minimum

Answer 1

Hint: We will use Snell’s law and expression for finding the refractive index of a prism to solve this question. Snell’s law states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction gives the refractive index of the medium. The Refractive index is a dimensionless quantity that describes the speed of light traveling through any material.
Formula Used:
$\mu =\dfrac{\sin \left( \dfrac{A+{{\delta }_{m}}}{2} \right)}{\sin \left( \dfrac{A}{2} \right)}$
$\mu =\dfrac{\sin (i)}{\sin \left( r \right)}$

Complete step-by-step solution:
First of all, we will draw a diagram for refraction in an equilateral prism, so we can understand all the angles better.

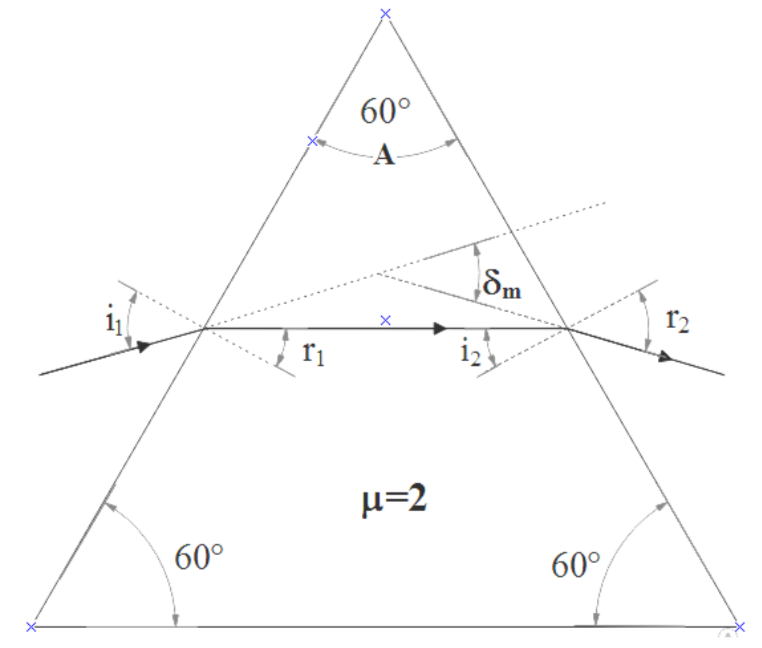
Here, ${{i}_{1}}$ is the angle of incidence for the first refraction.
           ${{i}_{2}}$ is the angle of incidence for the second refraction.
           ${{r}_{1}}$ is the angle of refraction for the first refraction.
           ${{r}_{2}}$ is the angle of refraction for the second refraction.
           $A$ is the angle of the prism.
           ${{\delta }_{m}}$ is the angle of minimum deviation.
   And $\mu $ is the refractive index of prism.
In the question, it is given that,
Refractive index or prism as $\mu =\sqrt{2}$ .
The given prism is an equilateral prism. So, the angle of the prism is A will be $60{}^\circ $.
Now we have to find the value of minimum deviation. We know that minimum deviation is denoted by ${{\delta }_{m}}$.
So we will use the formula which gives the relation between refractive index and minimum derivation for a prism,
$\mu =\dfrac{\sin \left( \dfrac{A+{{\delta }_{m}}}{2} \right)}{\sin \left( \dfrac{A}{2} \right)}$
By giving the values of A as $60{}^\circ $ and $\mu =\sqrt{2}$,
 $\begin{align}
  & \Rightarrow \sqrt{2}=\dfrac{\sin \left( \dfrac{{{60}^{{}^\circ }}+{{\delta }_{m}}}{2} \right)}{\sin \left( \dfrac{{{60}^{{}^\circ }}}{2} \right)} \\
 & \Rightarrow \sqrt{2}\times \sin \left( \dfrac{{{60}^{{}^\circ }}}{2} \right)=\sin \left( \dfrac{{{60}^{{}^\circ }}+{{\delta }_{m}}}{2} \right) \\
 & \Rightarrow \sqrt{2}\times \sin \left( 30{}^\circ \right)=\sin \left( \dfrac{{{60}^{{}^\circ }}+{{\delta }_{m}}}{2} \right) \\
 & \Rightarrow \dfrac{1}{\sqrt{2}}=\sin \left( \dfrac{{{60}^{{}^\circ }}+{{\delta }_{m}}}{2} \right) \\
 & \Rightarrow {{\sin }^{-1}}\left( \dfrac{1}{\sqrt{2}} \right)=\dfrac{{{60}^{{}^\circ }}+{{\delta }_{m}}}{2} \\
 & \Rightarrow {{45}^{{}^\circ }}=\dfrac{{{60}^{{}^\circ }}+{{\delta }_{m}}}{2} \\
 & \Rightarrow {{\delta }_{m}}=90{}^\circ -60{}^\circ =30{}^\circ \\
\end{align}$
Hence the minimum deviation is $30{}^\circ $ .
Therefore, Option A is correct and option B is wrong.
Now we have to find the minimum deviation.
By considering geometry in the figure, we can deduce that ${{\delta }_{m}}={{r}_{1}}=\left( {{r}_{2}}-\dfrac{A}{2} \right)$ .
Now, according to Snell’s law,
$\mu =\dfrac{\sin (i)}{\sin \left( r \right)}$
If we consider the first refraction, Snell’s law will be,
$\mu =\dfrac{\sin ({{i}_{1}})}{\sin \left( {{r}_{1}} \right)}$
And we know, $\mu =\sqrt{2}$ and ${{\delta }_{m}}=30{}^\circ ={{r}_{1}}$ .
So, we can write that,
$\begin{align}
  & \sin {{i}_{1}}=\mu \sin {{r}_{1}} \\
 & \Rightarrow \sin {{i}_{1}}=(\sqrt{2})\sin 30{}^\circ \\
 & \Rightarrow \sin {{i}_{1}}=(\sqrt{2})\times \dfrac{1}{2} \\
 & \Rightarrow {{i}_{1}}={{\sin }^{-1}}\left( \dfrac{1}{\sqrt{2}} \right) \\
 & \Rightarrow {{i}_{1}}=45{}^\circ \\
\end{align}$
Hence the angle of incidence is $45{}^\circ $ for an angle of deviation of $30{}^\circ $ . So Option C is true and Option D is wrong.
So, we can conclude that the minimum deviation from this prism can be $30{}^\circ $ and the angle of incidence or i is $45{}^\circ $ when the deviation is minimum.
Hence, the correct answers are Option A and Option C.

Note: We should not confuse reflection with refraction. This is because refraction determines the bending of the path of light while entering into a material while reflection determines the striking of light to a reflecting object and the path of light moving away from the reflecting object. Reflection occurs within the same medium.