Question

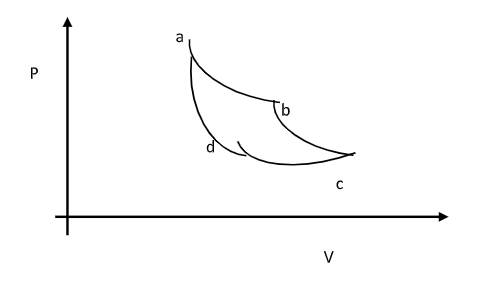
Refer to the carnot cycle of an ideal gas shown in the figure Let \[{W_{a \to b}},{W_{b \to c}},{W_{c \to d}} \;and\; {W_{d \to a}}\] represent the work done by the system during the processes \[a \to b,b \to c,c \to d\] and \[d \to a\] respectively . consider the following relations-

(1) \[{W_{a \to b}} + {W_{b \to c}} + {W_{c \to d}} + {W_{d \to a}} > 0\]
(2) \[{W_{a \to b}} + {W_{b \to c}} + {W_{c \to d}} + {W_{d \to a}} < 0\]
(3) \[{W_{a \to b}} + {W_{c \to d}} > 0\]
(4) \[{W_{b \to c}} + {W_{d \to a}} = 0\]
Which of the above relation is/are true?
(A) 1 and 3 only
(B) 3 and 4 only
(C) 1,3 and 4 only
(D) 2,3 and 4 only

Answer 1

Hint: It’s a carnot cycle so out of those four processes 2 (more specifically \[a \to b\&\; c \to d\]) are isothermal process and the rest are adiabatic process and since its an P-V graph, area under the loop will give us work done.

Complete step by step answer: Since the entire cyclic loop is anti-clock wise it means work done by gas or system on surrounding will be positive,
We can also answer this intuitively
Let's take the processes \[a \to b\] and \[ b \to c\] the gas is expanding in these two processes so work done by system will be positive now take the processes \[c \to d\] and \[d \to a\] gas is compressing in these two processes so work done by the system will be negative but if you look at the values of pressure in both cases it is clear that magnitude of pressure in 1st two processes were larger so overall total work done will be positive so part-(1) is correct.
Now in \[a \to b\] \[ c \to d\] both the processes are isothermal but magnitude of pressure in \[a \to b\] is greater than in \[c \to d\] so overall work done will be positive in these two cases
ie, \[{W_{a \to b}} + {W_{c \to d}} > 0\]
so part-(3) is also correct
in processes \[b \to c\] and \[d \to a\] both these processes are adiabatic so there will be no exchange of heat in these two processes and work done in these two process will also be zero because temperature difference in both cases is same and since its adiabatic change in internal energy will be same as work done which is same as temperature difference is same
so part-(4) is also correct.

Hence, Option-C is correct.

Note: In such type of questions you can definitely form equations and solve and then find the correct option but sometimes intuition with the basic understanding of the thermodynamics can also give you correct answer with very less time which will be much helpful when you are writing some competitive exam.