Question

Rectangle ABCD has area 200. An ellipse with area $200\pi$ passes through A and C and has foci at B and D. Find the perimeter of the rectangle.

Answer 1

Hint: We should have a basic understanding of ellipses and the terminologies related to them to solve this question. We start to solve this question by equating $\Rightarrow \pi ab=200\pi$ . Then, we find the values of $x,y\;$ by deriving an equation in $x,y,a,b\;$ . Lastly, we find the perimeter of the rectangle using the formula $2\left( x+y \right)$ .

Complete step by step solution:
We are given the area of the rectangle ABCD and the area of the ellipse passing through it and need to find the perimeter of the rectangle.
The given question can be diagrammatically represented as follows,

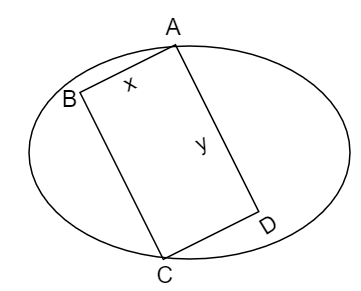
The area of the ellipse that passes through A and C and has foci at B and D is given by $200\pi$.
Let us consider the length and the breadth of the rectangle to be $x,y\;$ respectively.
From geometry,
We know that the length of the major axis of the ellipse is $2a\;$ and the length of the minor axis is $2b\;$ .
The area of an ellipse is given by the formula $\pi ab$
Equating both the areas of eclipse, we get,
$\Rightarrow \pi ab=200\pi$
Simplifying the above equation, we get,
$\Rightarrow ab=200$
$\therefore xy=200$
From geometry, we know that the length of the diagonal of the rectangle can be given as $\sqrt{{{x}^{2}}+{{y}^{2}}}$and $x+y=2a$
Comparing the length of the axes and the distance from the foci to the center, we get,
$\Rightarrow {{a}^{2}}=\dfrac{{{x}^{2}}+{{y}^{2}}}{4}+{{b}^{2}}$
Taking LCM on both sides, we get,
$\Rightarrow {{(x+y)}^{2}}={{x}^{2}}+{{y}^{2}}+4{{b}^{2}}$
Expanding the square on the left-hand side of the equation, we get,
$\Rightarrow {{x}^{2}}+{{y}^{2}}+2xy={{x}^{2}}+{{y}^{2}}+4{{b}^{2}}$
Cancelling the same terms on either side of the equation, we get,
$\Rightarrow 2xy=4{{b}^{2}}$
From the above, we know that $xy=200$
Substituting the same, we get,
$\Rightarrow 2\times 200=4{{b}^{2}}$
Simplifying the above equation, we get,
$\Rightarrow 400=4{{b}^{2}}$
On further simplifying the above equation, we get
$\Rightarrow 100={{b}^{2}}$
Taking the square root on both sides of the equation, we get,
$\Rightarrow \sqrt{100}=\sqrt{{{b}^{2}}}$
$\therefore b=10$
We know that,
$\Rightarrow ab=200$
Substituting the value of $b$ in the equation, we get,
$\Rightarrow a\times 10=200$
Simplifying the above equation, we get,
$\therefore a=20$
From the above,
$\Rightarrow x+y=2a$ and $xy=200$
We need to find the value of $x,y\;$
$\Rightarrow xy=200$
$\Rightarrow y=\dfrac{200}{x}$
Substituting the value of $y=\dfrac{200}{x}$ in the equation, we get,
$\Rightarrow x+\dfrac{200}{x}=2a$
Substituting the value of $a$ , we get,
$\Rightarrow x+\dfrac{200}{x}=2\times 20$
Simplifying the above equation, we get,
$\Rightarrow {{x}^{2}}+200=40x$
$\Rightarrow {{x}^{2}}-40x+200=0$
Finding the roots for the above quadratic expression, we get,
$\Rightarrow x=20\pm 10\sqrt{2}$
$\Rightarrow x=20-10\sqrt{2}$ or $x=20+10\sqrt{2}$
Finding the value of $y$ , we get,
$\Rightarrow x+y=40$
$\Rightarrow \left( 20-10\sqrt{2} \right)+y=40$
$\therefore y=20+10\sqrt{2}$
$\Rightarrow \left( 20+10\sqrt{2} \right)+y=40$
$\therefore y=20-10\sqrt{2}$
Perimeter of the rectangle is given by the formula $2\left( x+y \right)$ where $x,y\;$ are the lengths of the sides of the rectangle.
Here,
$x=20-10\sqrt{2}$ or $20+10\sqrt{2}$
$y=20+10\sqrt{2}$ or $20-10\sqrt{2}$
We can substitute any value of $x,y\;$ from the above corresponding two values.
$\Rightarrow \text{Perimeter}$$=2(x+y)$
$\Rightarrow \text{Perimeter = 2}\left( \left( 20-10\sqrt{2} \right)+\left( 20+10\sqrt{2} \right) \right)$
Simplifying the above equation, we get,
$\Rightarrow \text{Perimeter = 2}\left( 20+20 \right)$
$\Rightarrow \text{Perimeter = 2}\left( 40 \right)$
$\therefore \text{Perimeter = 80}$
Hence, the perimeter of the rectangle which has an ellipse passing through its vertex A and C is $80\;$ units.

Note: An ellipse in mathematics can be defined as a plane curve that surrounds two focal points, such that the sum of the two distances to the focal points for all the points of the curve is constant.
We need to keep in mind that the correct formula has to be applied and the values substituted should be correct while solving these questions.