Question

How can I read the potential energy diagrams when there is thermal energy?

Answer 1

Hint: The best way to read the potential energy is by comparing the height of the barrier to the average thermal energy. In this case, the average thermal energy will be kT.

Complete answer:
In order to answer our question, we need to learn about the potential energy diagrams, as well as the concept of activation energy and its relation with the rate constant of a reaction. Let us now consider the effect of increase in temperature on the number of effective collisions .When the temperature increases the kinetic energy of molecules increases ( $K.E\,\alpha \,T$) therefore, most of the energy distribution curve gets flattened out and shifts towards higher energy value i.e., shifts to right as there is now greater proportion of molecules with much higher energies. On the basis of probability consideration Fig. 4.9 is drawn to give the energy distribution curves at temperatures ${{T}_{1}}$ and ${{T}_{2}}$ (where ${{T}_{2}}={{T}_{1}}+10$). A close examination of the curves in the graph clearly reveals that the fraction of molecules possessing higher kinetic energy, i.e., energy greater than threshold energy, as indicated by shaded portion becomes almost double and therefore the rate of reaction almost doubles for ${{10}^{0}}$ rise of temperature. Thus, an increase in the rate of reaction with increase in temperature is mainly due to an increase in the number of collisions which are energetically effective. Let us see energy distribution at different temperatures:

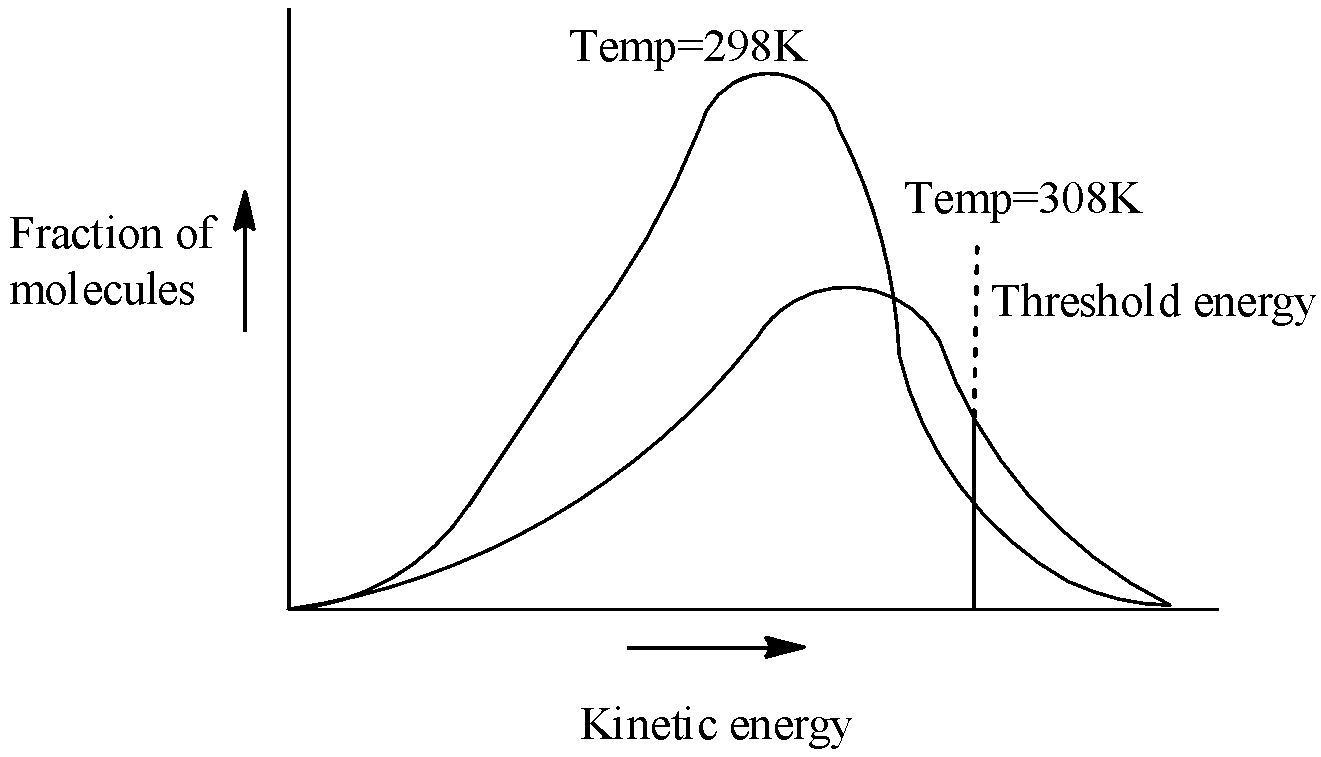
Now, an interesting observation has been made by Arrhenius and Boltzmann which shows us the height of the potential barrier. If k is the rate constant, ${{E}_{a}}$ is the activation energy, T is temperature and R be the universal gas constant, then:
\[k={{e}^{\dfrac{-{{E}_{a}}}{RT}}}\]

Note:
In the formula, sometimes a pre exponential factor is also included, which can be also said as the frequency factor. The differential form of the equation can be written as:$\dfrac{d\,\ln k}{dT}=\dfrac{E}{R{{T}^{2}}}$.