Question

Rays OA, OB, OC, OD and OE have the common endpoint O. Show, that
\[\angle AOB{\text{ }} + \angle BOC{\text{ }} + \angle COD{\text{ }} + \angle DOE{\text{ }} + \angle EOA{\text{ }} = {\text{ }}360^\circ \].
               

Answer 1

Hint: A linear pair is a pair of adjacent, supplementary angles. Adjacent means next to each other, and supplementary means that the measures of the two angles add up to equal 180 degrees. We are going to form a linear pair in the solution and then will prove the identity given.

Complete step-by-step answer:
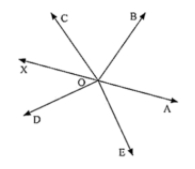
Consider the attached figure while going through the following steps.

From given, we have,

The rays OA, OB, OC, OD and OE have the common end point O.

Draw a ray OX opposite to that of ray OA.

A ray opposite to OA is drawn, which makes a straight line AX.

From figure, since \[\angle AOB, \angle BOX\] are linear pairs of the ray OA and OX,
(Two adjacent angles are said to form a linear pair of angles, if their non-common arms are two opposite rays.)

\[\angle AOB{\text{ }} + \angle BOX{\text{ }} = {\text{ }}180^\circ \]
\[\angle AOB{\text{ }} + \angle BOC{\text{ }} + \angle COX{\text{ }} = {\text{ }}180^\circ \;\].... (1)

Also,\[\angle AOE{\text{ }} and \angle EOX\] are linear pairs of the ray OA and OX
(Two adjacent angles are said to form a linear pair of angles, if their non-common arms are two opposite rays.)


\[\angle AOE{\text{ }} + \angle EOX{\text{ }} = {\text{ }}180^\circ \]
\[\angle AOE{\text{ }} + \angle DOX{\text{ }} + \angle DOE{\text{ }} = {\text{ }}180^\circ \;\].... (2)

Now we will be adding (1) and (2) equations to get below mentioned equation:

\[\angle AOB{\text{ }} + \angle BOC{\text{ }} + \angle COX{\text{ }} + \angle AOE{\text{ }} + \angle DOX{\text{ }} + \angle DOE{\text{ }} = {\text{ 36}}0^\circ \]
(Since \[\angle COX{\text{ }} + \angle DOX = \angle COD\])
\[\angle AOB{\text{ }} + \angle BOC{\text{ }} + \angle COD{\text{ }} + \angle DOE{\text{ }} + \angle EOA{\text{ }} = {\text{ 36}}0^\circ \]

Hence proved.

Note: Two angles are supplementary if the sum of their angles equals \[180^\circ\].
If one angle is known, its supplementary angle can be found by subtracting the measure of its angle from \[180^\circ\].
The triangle angles are not supplementary in spite of being \[180^\circ\] in sum as they are three angles.