Question

Rate of dissipation of Joule’s heat in resistance per unit volume is (symbols have useful meaning).
(A) $ \sigma E $
(B) $ \sigma J $
(C) $ JE $
(D) None

Answer 1

Hint :Here, the rate of dissipation is asked for a resistor. So, we have to understand the concept of rate of dissipation that the dissipation is the result of the irreversible process that takes place in homogeneous thermodynamic systems. Heat flows through a thermal resistance in a conductor because of electrical current flow through an electrical resistance (Joule heating).This dissipation rate we have to calculate for a resistor.

Complete Step By Step Answer:
Consider the resistor to obtain the rate of dissipation of joule’s heat in resistance per unit volume with length $ L $ and resistance $ R $ also the area of that resistor as $ A $ as shown in figure:

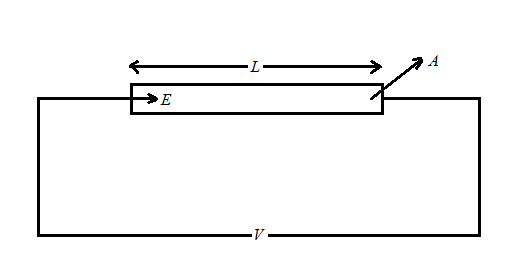
The potential applied to the resistance with length $ L $ and the direction of the current is given by $ E $ .
Thus, the voltage is given by $ V = EL $
Heat in the resistor is given by
 $ P = \dfrac{{{V^2}}}{R} $
 $ \Rightarrow P = \dfrac{{{{\left( {EL} \right)}^2}}}{{\left( {\dfrac{{\rho L}}{A}} \right)}} $ …. (use $ V = EL $ and $ R = \dfrac{{\rho L}}{A} $ )
 $ \Rightarrow P = \dfrac{{{E^2}AL}}{\rho } $ …. $ (1) $
Now, let $ v $ be the volume of the resistor such that $ v = AL $
In equation $ (1) $ we have to put the volume $ v $
 $ \Rightarrow P = \sigma {E^2}v $ …. (Since, $ \sigma = \dfrac{1}{\rho } $ )
Thus, the rate of dissipation of joule’s heat per unit volume is given by:
 $ \Rightarrow \dfrac{P}{v} = \sigma {E^2} $
 $ \Rightarrow \dfrac{P}{v} = \sigma E.E = JE $ …. (Since, $ J = \sigma E $ )
Here, $ J $ is the current density.
Therefore, the answer we have obtained is that the rate of dissipation per unit volume is given by:
 $ \dfrac{P}{v} = JE $
Therefore, the answer is option C.

Note :
Here, we have discussed the rate of dissipation of heat in the resistor as above. So, we have calculated the heat per unit volume rate as $ JE $ and here, $ J $ is the current density of the conductor and $ E $ is the electrical energy produced in the resistor. We must know the concept of heat and energy in thermodynamics.