Question

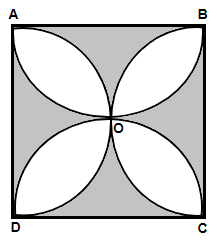
Rashmi made a rangoli design in a rangoli competition. She came first in the competition because she made perfect size rangoli. She measured every part while making rangoli, it is a square side 14 cm. Semi – circles are drawn with each side of the square as diameter. Find the area of the shaded region. Use $\left( \pi =\dfrac{22}{7} \right)$.

Answer 1

Hint: First of all find the radius (r) of each semicircle by considering the length of the side of the square as the diameter d. Use the formula $r=\dfrac{d}{2}$.Now, to find the area of the shaded region subtract the area of the four semi – circles from two times the area of the square and get the answer. Use the formulas: - Area of a square = ${{\left( \text{side} \right)}^{2}}$ and area of a semi – circle $=\dfrac{\pi {{r}^{2}}}{2}$.

Complete step by step answer:
Here we are asked to find the area of the shaded region of the rangoli that is made by Rashmi in a competition. Let us shade the required part with two different colors for better understanding.

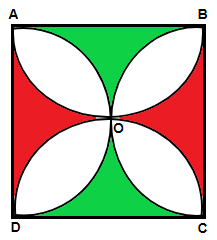
Now, we can see that the side of square is acting as the diameter of the semi – circle. So let us assume the side length equal to the diameter (d) and the radius of each semi – circle as (r). We know that we have following relation between the radius and diameter of a circle: -
$\Rightarrow r=\dfrac{d}{2}.............\left( i \right)$
Let us come to the figure. Think that what will happen if we will subtract area of the two semi – circles AOB and COD from the area of the square. The answer is will get the area of the two red parts. Further if we will subtract the area of the two semi – circles AOD and BOC then we will get the area of the two green parts. Therefore, the required area of the whole shaded part will be given as: -
$\Rightarrow $ Area of the shaded part = Area of Square ABCD – Area of semi – circles (AOB + COD) + Area of Square ABCD – Area of semi – circles (AOD + BOC)
$\Rightarrow $ Area of the shaded part = 2 $\times $ Area of Square ABCD – Area of semi – circles (AOB + COD + AOD + BOC)
Since area of all the semi – circles are equal so we can write the above relation as: -
$\Rightarrow $ Area of the shaded part = 2 $\times $ Area of Square ABCD – 4 $\times $ Area of semi – circle (AOB)
Using the formulas Area of a square = ${{\left( \text{side} \right)}^{2}}$ and area of a semi – circle $=\dfrac{\pi {{r}^{2}}}{2}$ we get,
$\Rightarrow $ Area of the shaded part = $2\times {{d}^{2}}-4\times \dfrac{\pi {{r}^{2}}}{2}$
Using relation (i) we get,
$\Rightarrow $ Area of the shaded part = $2\times {{d}^{2}}-2\times \pi {{\left( \dfrac{d}{2} \right)}^{2}}$
$\Rightarrow $ Area of the shaded part = $2\times {{d}^{2}}-\dfrac{\pi \times {{d}^{2}}}{2}$
$\Rightarrow $ Area of the shaded part = ${{d}^{2}}\left( 2-\dfrac{\pi }{2} \right)$
Substituting the value of d = 14 and $\pi =\dfrac{22}{7}$ we get,
$\Rightarrow $ Area of the shaded part = ${{\left( 14 \right)}^{2}}\left( 2-\dfrac{22}{2\times 7} \right)$
On simplification we get,
$\therefore $ Area of the shaded part = $84c{{m}^{2}}$
Hence, the area of the shaded part is 84 square cm.

Note: You must think of the solution of the problem geometrically because there is no direct formula regarding the above question. These types of problems are included in analytical geometry. It is already understood that the area of each shaded part will be equal because the figure will be symmetric. Remember the formulas of area of all the basic shapes like circle, square, rectangle etc.