Question

Ramesh wants to design a rectangular park of perimeter 80 m and area of \[400{{m}^{2}}\] for jogging and morning walk for the people of his colony. Is it possible to design a park? If so find the length and breadth of the park. Which value of Ramesh is depicted here?

Answer 1

Hint: We know that if the length of the park is equal to l and the breadth of the park is equal to b then the perimeter of the rectangle is equal to \[2\left( l+b \right)\] and the area of the rectangle is equal to \[lb\]. From the question, it is given that a rectangular park perimeter is equal to 80 m and area of \[40{{m}^{2}}\]. So, by using this concept, we can find whether the design of a rectangular park is possible or not.

Complete step-by-step answer:
From the question, it is given that a rectangular park perimeter is equal to 80 m and area of \[400{{m}^{2}}\].
We know that if the length of the park is equal to l and the breadth of the park is equal to b then the perimeter of the rectangle is equal to \[2\left( l+b \right)\] and the area of the rectangle is equal to \[lb\].

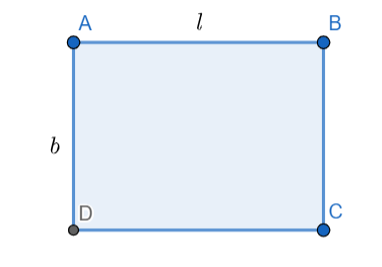
So, from the question we can write
\[\begin{align}
  & \Rightarrow 2\left( l+b \right)=80....(1) \\
 & \Rightarrow lb=400....(2) \\
\end{align}\]
Now from equation (1), we get
\[\begin{align}
  & \Rightarrow l+b=\dfrac{80}{2} \\
 & \Rightarrow l+b=40 \\
 & \Rightarrow l=40-b...(3) \\
\end{align}\]
Now we should substitute equation (3) in equation (2), then we get
\[\begin{align}
  & \Rightarrow \left( 40-b \right)b=400 \\
 & \Rightarrow 40b-{{b}^{2}}=400 \\
 & \Rightarrow {{b}^{2}}-40b+400=0 \\
\end{align}\]
We know that the roots of the quadratic equation \[a{{x}^{2}}+bx+c\] are equal to \[\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\].
\[\begin{align}
  & \Rightarrow b=\dfrac{-\left( -40 \right)\pm \sqrt{{{\left( -40 \right)}^{2}}-4\left( 1 \right)\left( 400 \right)}}{2\left( 1 \right)} \\
 & \Rightarrow b=\dfrac{40\pm \sqrt{1600-1600}}{2} \\
 & \Rightarrow b=\dfrac{40\pm 0}{2} \\
 & \Rightarrow b=\dfrac{40}{2} \\
 & \Rightarrow b=20m \\
\end{align}\]
So, it is clear that we can take the value of b as 20 m and construct a park.
Therefore, we will have the breadth of the park as 20 m and length as $\dfrac{400}{20}=20$ m.
Ramesh is a responsible citizen and cares about the well being of his community. This quality of Ramesh is being depicted here.

Note: Students must note that it is not necessary that they will have only one value of b always. If they had got 2 values of b, then they must check if it is > 0 because the dimensions of a park cannot be negative. After getting the value of b, here we have actually got both length and breadth to be the same, i.e 20 m. So, here students usually start doubting the solution since in the question it is mentioned about a rectangular park. But, they must not get confused with that and proceed with the obtained values if they are sure about their calculations.