Question

Ram and Shyam are walking on two perpendicular tracks with speed $3m{s^{ - 1}}$ and $4m{s^{ - 1}}$ respectively. At a certain moment (say $t = 0\sec $) Ram and Shyam are $20m$ and $10m$ away from the intersection of tracks respectively and moving towards the intersection of the tracks. Shortest distance between them subsequently is:
A. $18m$
B. $15m$
C. $25m$
D. $8m$

Answer 1

Hint:Here, we need to find the shortest distance between Ram and Shyam. For this, we will first find the relative displacement between Ram and shyam at a certain time in terms of time $t$ . After that, we will derive this displacement with respect to time and equate it to zero because when the derivative is zero, we get the minimum distance. By doing this, we can determine the time when the distance between Ram and Shyam is the shortest and using this value, we will get the required distance.

Formula used:
$v = \dfrac{d}{t}$
Where $v$ is the velocity, $d$ is the distance and $t$ is the time

Complete step by step answer:

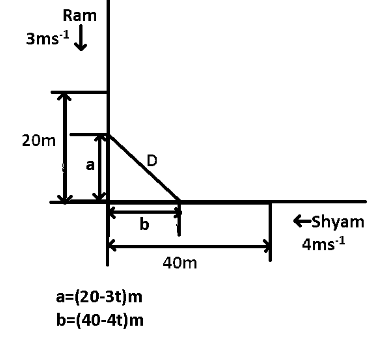
Let us assume that after $t$ second, the distance between Ram and Shyam $D$ is the shortest. Now, distance covered by Ram and Shyam after $t$ second can be determined by using the formula $v = \dfrac{d}{t}$
Here, it is given that Ram and Shyam are walking on two perpendicular tracks with speed $3m{s^{ - 1}}$and $4m{s^{ - 1}}$ respectively,

Therefore, the distance covered by Ram in $t$ second is $\left( {3t} \right)m$ and the remaining distance to reach the intersection is $\left( {20 - 3t} \right)m$. And the distance covered by Shyam in $t$ second is $\left( {4t} \right)m$ and the remaining distance to reach the intersection is $\left( {40 - 4t} \right)m$. Now, as shown in the figure we can determine the distance D by using the law of Pythagoras.
$D = \sqrt {{{\left( {20 - 3t} \right)}^2} + {{\left( {40 - 4t} \right)}^2}} $
To get the minimum value of $D$we will equate its derivative with respect to $t$ to zero
\[
\dfrac{{dD}}{{dt}} = 0 \\
\Rightarrow \dfrac{{ - 6\left( {20 - 3t} \right) - 8\left( {40 - 4t} \right)}}{{2\sqrt {{{\left( {20 - 3t} \right)}^2} + {{\left( {40 - 4t} \right)}^2}} }} = 0 \\
\Rightarrow - 6\left( {20 - 3t} \right) - 8\left( {40 - 4t} \right) = 0 \\
\Rightarrow - 120 + 18t - 320 + 32t = 0 \\
\Rightarrow 50t = 440 \\
\Rightarrow t = 8.8\sec \\
\]
Putting this value to find $D$, we get
$
D = \sqrt {{{\left( {20 - 3 \times 8.8} \right)}^2} + {{\left( {40 - 4 \times 8.8} \right)}^2}} \\
\Rightarrow D = \sqrt {40.96 + 23.04} \\
\Rightarrow D = \sqrt {64} \\
\therefore D = 8m \\ $
Thus, the shortest distance between Ram and Shyam subsequently is $8m$.

Hence, option D is the right answer.

Note:In this question, we have used a concept of finding the minimum value of the distance by equating its derivative with respect to time to zero. This method is very useful in many cases to find the maximum or minimum value of a function. By doing this, we can find the point at which the function has minimum or maximum value (as we have determined $t = 8.8\sec $) and then by putting this value in the function, we can get the maximum or minimum value ( as we have determined $D = 8m$) of that function.