Question

Rain is falling with the speed of $25\sqrt 3 {\text{ }}m/s$ vertically. The wind blows west to east at a speed of 25 m/s. Find the velocity of rain as experienced by a person standing on ground:
${\text{A}}{\text{. 50 m/s}}$
${\text{B}}{\text{. 100 m/s}}$
${\text{C}}{\text{. 0 m/s}} $
${\text{C}}{\text{. 90 m/s}} $

Answer 1

Hint: We need to treat the direction of the rain falling down and the direction of the wind as the two vectors. Then drawing the diagram for these vectors, we can get the velocity of rain as experienced by a person standing on ground to be the resultant of two vectors.

Formula used:

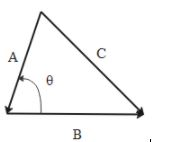
If we have two vectors A and B as shown in the figure then the magnitude of the resultant C is given as
$C = \sqrt {{A^2} + {B^2} + 2AB\cos \theta } $
Here $\theta $ is the angle between vectors A and B.

Complete step-by-step answer:
If we treat the velocities of the rain and that of the wind to be vectors then we can draw the following diagram where ${V_r}$ is the velocity of the rain falling downwards while ${V_w}$ is the velocity of the wind blowing from west to the east direction.

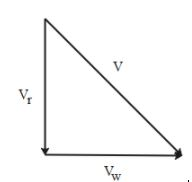
The resultant of these two velocities is equal to V which is the velocity of rain as experienced by a person standing on ground.
We are given the velocities of the rain and of the wind as follows:
$
  {V_r} = 25\sqrt 3 m/s \\
  {V_w} = 25m/s \\
$
The angle between these vectors is equal to $90^\circ $. Therefore, the resultant of these two vectors is given as
$
  V = \sqrt {V_r^2 + V_w^2 + 2{V_r}{V_w}\cos 90^\circ } \\
   = \sqrt {V_r^2 + V_w^2 + 0} \\
   = \sqrt {{{\left( {25\sqrt 3 } \right)}^2} + {{\left( {25} \right)}^2}} \\
   = 25\sqrt {3 + 1} = 25\sqrt 4 \\
   = 25 \times 2 = 50m/s \\
$
This is the value of the velocity of rain as experienced by a person standing on ground.

So, the correct answer is “Option A”.

Note: The person moving in rain with wind blowing experiences only the resultant of the two vectors. There is an increase in the velocity of the rain drops due to the wind pushing on the raindrops as can be seen from the answer obtained in this question.