Question

Rain is falling vertically at speed of $10m/s$ and a man is moving with velocity $6m/s$. Find the angle at which the man should hold his umbrella to avoid getting wet.
A. ${\sin ^{ - 1}}\left( {\dfrac{3}{5}} \right)$
B. ${\cos ^{ - 1}}\left( {\dfrac{3}{5}} \right)$
C. ${\tan ^{ - 1}}\left( {\dfrac{4}{5}} \right)$
D. ${\tan ^{ - 1}}\left( {\dfrac{3}{5}} \right)$

Answer 1

Hint:Here, speed of rain and velocity of man is given. We know that rain falls vertically downwards and we consider that ma is moving in the left to right direction. We need to find the relative velocity of rain with respect to man to determine the angle at which the man should hold his umbrella to avoid getting wet.

Formulas used:
\[\overrightarrow {{v_{AB}}} = \overrightarrow {{v_A}} - \overrightarrow {{v_B}} \] ,
where, \[\overrightarrow {{v_{AB}}} \] is the relative velocity of A with respect to B, \[\overrightarrow {{v_A}} \] is the velocity of A and \[\overrightarrow {{v_B}} \] is the velocity of B.

Complete step by step answer:
It is given that Rain is falling vertically at a speed of $10m/s$and a man is moving with velocity $6m/s$.

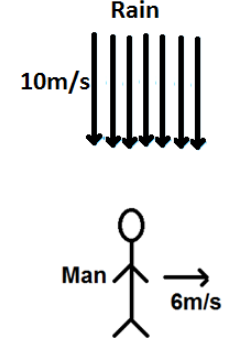
From the figure, we can say that
Velocity of rain $\overrightarrow {{v_r}} = - 10\widehat jm/s$and velocity of man $\overrightarrow {{v_m}} = 6\widehat im/s$
Now, we will find the relative velocity of rain with respect to man.
By using the formula \[\overrightarrow {{v_{AB}}} = \overrightarrow {{v_A}} - \overrightarrow {{v_B}} \],
\[\overrightarrow {{v_{rm}}} = \overrightarrow {{v_r}} - \overrightarrow {{v_m}} \], where, \[\overrightarrow {{v_{rm}}} \] is the relative velocity of rain with respect to man
\[\overrightarrow {{v_{rm}}} = \overrightarrow {{v_r}} - \overrightarrow {{v_m}} = - 10\widehat j - 6\widehat i\]
If we draw a vector diagram for this relative velocity of rain with respect to man, we get

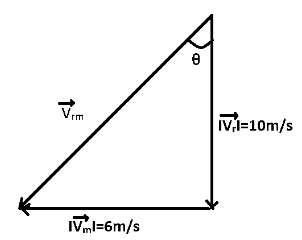
The direction of the relative velocity of rain with respect to man should be the direction of holding an umbrella. From the figure,
$
\tan \theta = \dfrac{6}{{10}} \\
\Rightarrow \tan \theta = \dfrac{3}{5} \\
\Rightarrow \theta = {\tan ^{ - 1}}\left( {\dfrac{3}{5}} \right) \\ $
This angle is vertical.

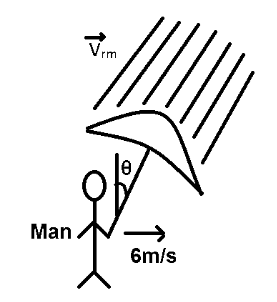
Thus, as shown in figure, a man should hold the umbrella with the angle $\theta = {\tan ^{ - 1}}\left( {\dfrac{3}{5}} \right)$ to avoid getting wet.

Hence, option D is the right answer.

Note:Here we have used the concept of relative velocity to determine the angle at which the man should hold his umbrella to avoid getting wet. The difference between velocity and relative velocity is that velocity is measured with respect to a reference point which is relative to a different point. Whereas, relative velocity is measured in a frame where an object is either at rest or moving with respect to the absolute frame.