Question

How many radial nodes are present in the $ 3s $ orbital?

Answer 1

Hint: Find out the quantum numbers associated with the given orbital and use those quantum numbers to determine the number of radial nodes present in a particular orbital. Remember that all quantum numbers are not needed for radial note calculation.

Complete answer:
Each electron in an atom can be uniquely identified on the basis of its quantum numbers. No two electrons in an atom can have the same set of all four quantum numbers. Different quantum numbers provide different information about the position of an electron inside the atom.
The principal quantum number $ n $ tells us about the energy level i.e. the number of shells present in an atom.
The azimuthal quantum number $ l $ tells us the shape of the orbital and gives us information regarding the subshells present in an atom.
The s-orbital is perfectly spherical in nature and symmetrical around all the three axes.
Orbitals define the three dimensional spaces that are accessible to the electrons. Nodes are the empty spaces in between the orbitals that have zero probability of finding an electron.
Nodes can be angular or radial in nature. Radial nodes define spaces in between the orbitals of consecutive principal quantum numbers where electrons cannot be positioned.

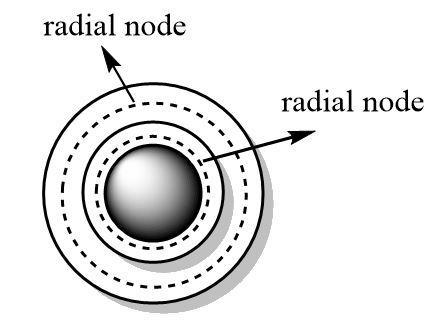
The formula for calculating the number of radial nodes is as follows:
 $ {\text{radial nodes}} = n - l - 1 $
The $ 3s $ orbitals have the principal quantum number $ n = 3 $ and an s-subshell that has azimuthal quantum number $ l = 0 $ .
 $ {\text{radial nodes(3s)}} = 3 - 0 - 1 $
 $ {\text{radial nodes(3s)}} = 2 $
Hence, the number of radial nodes present in $ 3s $ orbital are two.

Note:
The quantum numbers defined for any orbital are not independent of each other. The azimuthal quantum number is always related to the principal quantum number and cannot have a value that exceeds the principal quantum number.