Question

Question: A student tries to raise a chain consisting of three identical links. Each link has a mass of \[300{\rm{ g}}\]. The three-piece chain is connected to a string and then suspended vertically, with the student holding the upper end of the string and pulling upward. Because of the student’s pull, an upward force of \[12{\rm{ N}}\] is applied to the chain by the string.
a. Draw a free-body diagram for each of the links in the chain and also for the entire chain considered a single body.
b. Use the results of part (a) and Newton’s laws to find (i) the acceleration of the chain and (ii) the force exerted by the top link on the middle link.

Answer 1

Hint: From the concept of Newton’s second law, we can write the expressions for the equilibrium of chain and rigid links. The force due to acceleration of the chain will act in direction opposite to its motion, and the product of mass and acceleration gives its value.

Complete step by step answer:
The mass of each link of the chain is \[m = 300{\rm{ g}} = 300{\rm{ g}} \times \left( {\dfrac{{{\rm{kg}}}}{{{\rm{1000 g}}}}} \right) = 0.3\;{\rm{kg}}\].
The upward force applied on the chain due to the student's pull is \[F = 12{\rm{ N}}\].

Assume:
The tension between link 1 and link 2 is \[{T_1}\].
The tension between link 2 and link 3 is \[{T_2}\].

(a) Due to mass of each link there is tension between all the link and weight due to mass m will act downwards so we can draw the free-body diagrams for link 1, link 2 and link 3 as shown below:

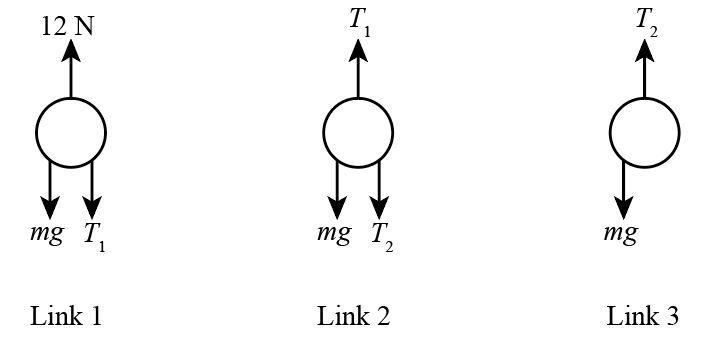
It is given that the chain is formed using three links each of mass m so we can write the mass of chain as three times the mass of one link.
\[M = 3m\]
Here M is the mass of the chain.

We will substitute \[0.3\;{\rm{kg}}\] for m in the above expression to find the value of the mass of the chain.
$
M = 3\left( {0.3\;{\rm{kg}}} \right)\\
 = 0.9\;{\rm{kg}}
$

It is also given that a pulling force F is acting on the chain whose value is given as \[12{\rm{ N}}\] which is acting upwards and weight of the chain ‘Mg’ will act downward so we draw the free-body diagram of the chain, considering it as a single body can be drawn as below:

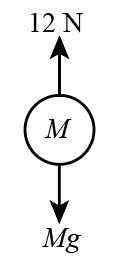
(b)
(i) Using the concept of Newton’s second law, we can write the equation of equilibrium for FBD of the chain as below:
\[12{\rm{ N}} - Mg = Ma\]
Here a is the acceleration of the chain with which it will move upwards, and g is the acceleration due to gravity whose value is given by \[9.81\;{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}}\].

We will substitute \[0.9\;{\rm{kg}}\] for M and \[9.81\;{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}}\] for g in the above expression to find the value of the acceleration of the chain.
$
12{\rm{ N}} - \left( {0.9\;{\rm{kg}}} \right)\left( {9.81\;{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}}} \right) = \left( {0.9\;{\rm{kg}}} \right)a\\
\implies 12{\rm{ N}} \times \left( {\dfrac{{{\rm{kg}}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}}{\rm{ }}}}{{\rm{N}}}} \right) - 8.829{\rm{ kg}}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}} = \left( {0.9\;{\rm{kg}}} \right)a\\
\implies a = 3.523{\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}}
$

(ii) Using the concept of Newton’s second law and concept of equilibrium, we can write the expression for link 1 as below:
\[12{\rm{ N}} - mg - {T_1} = ma\]

We will substitute \[0.3\;{\rm{kg}}\] for m and \[9.81\;{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}}\] for g and \[3.523{\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}}\] for a in the above expression.
$
12{\rm{ N}} - \left( {0.3\;{\rm{kg}}} \right)\left( {9.81\;{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}}} \right) - {T_1} = \left( {0.3\;{\rm{kg}}} \right)\left( {3.523{\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}}} \right)\\
\implies 12{\rm{ N}} \times \left( {\dfrac{{{\rm{kg}}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}}{\rm{ }}}}{{\rm{N}}}} \right) - 2.943{\rm{ kg}}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}} - {T_1} = 1.059{\rm{ kg}}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}}\\
\implies {T_1} = 7.998{\rm{ kg}}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}} \times \left( {\dfrac{{{\rm{ N}}}}{{{\rm{kg}}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}}}}} \right)\\
 = 7.998{\rm{ N}}
$

Therefore, the acceleration of the chain is \[3.523{\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}}\] and \[7.998{\rm{ N}}\] for \[7.998{\rm{ N}}\] is the force acting between the top link and middle link of the chain.

Note:
We can note that the acceleration of each link is the same as the acceleration of the chain because the chain can be considered as a rigid body. We can also remember the conversion of Newton into its base units (kg, m, s).