Question

What quadrilateral has two pairs of congruent sides, not including a parallelogram?

Answer 1

Hint: We know that opposite sides are congruent in a parallelogram. So in order to find other quadrilaterals with opposite sides that are congruent, we are supposed to examine the other quadrilateral properties too. We can examine the quadrilateral by checking if they are equal and when the figure is divided into equal halves, the opposite sides must line up on each other.

Complete step by step solution:
Now let us learn about the congruency. Congruence means having the same size and shape congruence triangles. To prove a quadrilateral is congruent, we have to put sides and interior angles of the quadrilateral in correspondence with sides and angles of others and to prove that all corresponding sides and angles are congruent. This conclusion helps us in proving that the quadrilaterals are congruent.
Now, let us find a quadrilateral that has two pairs of congruent sides other than parallelogram.
Let us examine the quadrilateral “kite”.
Properties of kite:
It has two pairs of consecutive and congruent sides.
It has congruent non vertex angles.
The diagonals bisect each other perpendicularly.
Sum of any two adjacent angles is \[{{180}^{\circ }}\].
The opposite angles are equal.
The opposite sides are parallel.
\[\therefore \] From the above properties listed of a kite, we can conclude that the kite has two pairs of congruent sides.

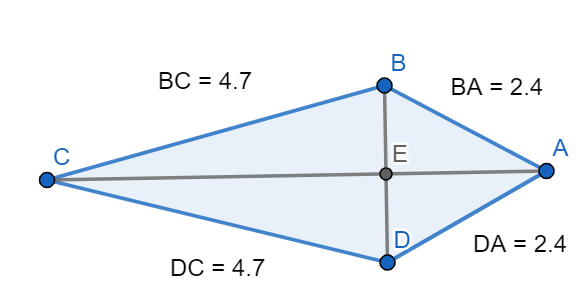
We can observe the above mentioned property from the above figure.

Note: Points to be remembered while proving the congruence. We can use the ASA postulate that is Angle-Side-Angle postulate which checks out the congruence by two angles and sides. We will also be able to prove that two angles have the same measures in both of the triangles which means that the third angle in both of the triangles have the same measure.