Question

Put three different numbers in the circles so that when you add the numbers at the end of each line you always get a perfect square.

Answer 1

Hint: We are required to fill the circles with numbers such that they pairwise sum up to be a perfect square. For this we need to be aware about the concept of perfect squares. After that we will find three such numbers which when filled inside the circles will complete the demand asked in the question.

Complete step by step answer:
A perfect square is a number that can be expressed as the product of two equal integers. For example, 49 is a perfect square because it is the product of two equal integers, $7\times 7=49$. However, 41 is not a perfect square because it cannot be expressed as the product of two equal integers.
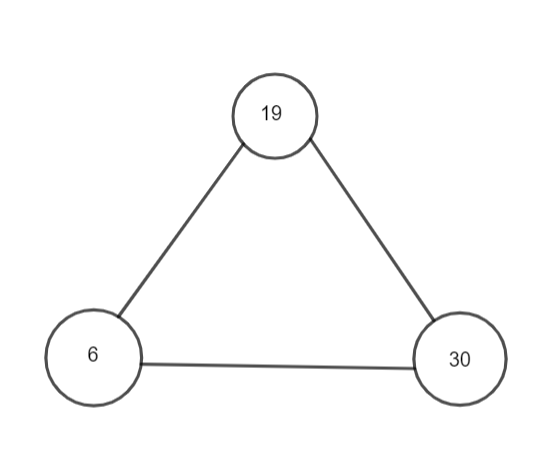
We start by filling one of the circles with 6. Adding 19 to this will give 25 which is a perfect square as $5\times 5=25$. Hence the second circle can be filled with 19. Now, if we add 30 to 19, we get 49 which is again a perfect square as $7\times 7=49$. Also, if 6 and 30 are added then 36 is produced which gives 36 which is also a perfect square since $6\times 6=36$. Hence, the three numbers that can be filled in the circles are 6,19 and 30.

Note: This question can have many possible solutions. One more possible set of triplets that will satisfy the given requirement is 5,20 and 44. We can clearly see that 5 and 20 sum up to be 25 which is a perfect square. 20 and 44 sum up to be 64 which is again a perfect square and 5 and 44 also sum up to be 49 which is a perfect square. So, this question has multiple solutions.