Question

PSQ is a focal chord of the parabola ${{y}^{2}}=8x$. If $SP=6$, then $\dfrac{SP}{SQ}=$

Answer 1

Hint: For this problem we need to calculate the ratio of $SP$ and $SQ$. For this first we will compare the given parabolic equation with the standard parabolic equation which is ${{y}^{2}}=4ax$ and calculate the value of $a$ accordingly. Now we have given that $PSQ$ is a focal chord of the given parabola. For parabola we have a semi latus rectum of a parabola is the harmonic mean between the segments of any focal chord of a parabola. So, we will calculate the value of the semi latus rectum of the parabola which is given by $2a$. After we can apply the above rule and calculate the value of $SQ$. Now we need to calculate the value of $\dfrac{SP}{SQ}$. So we will divide the value of $SP$ with the calculated value of $SQ$.

Complete step by step solution:
The Given equation of the parabola is ${{y}^{2}}=8x$.
Comparing the above equation of the parabola with the standard equation of the parabola which is ${{y}^{2}}=4ax$, then we will get
$\begin{align}
  & \Rightarrow 4a=8 \\
 & \Rightarrow a=2 \\
\end{align}$
In the problem they have mentioned that $PSQ$ is a focal chord of the parabola. Now the diagram of the parabola will be

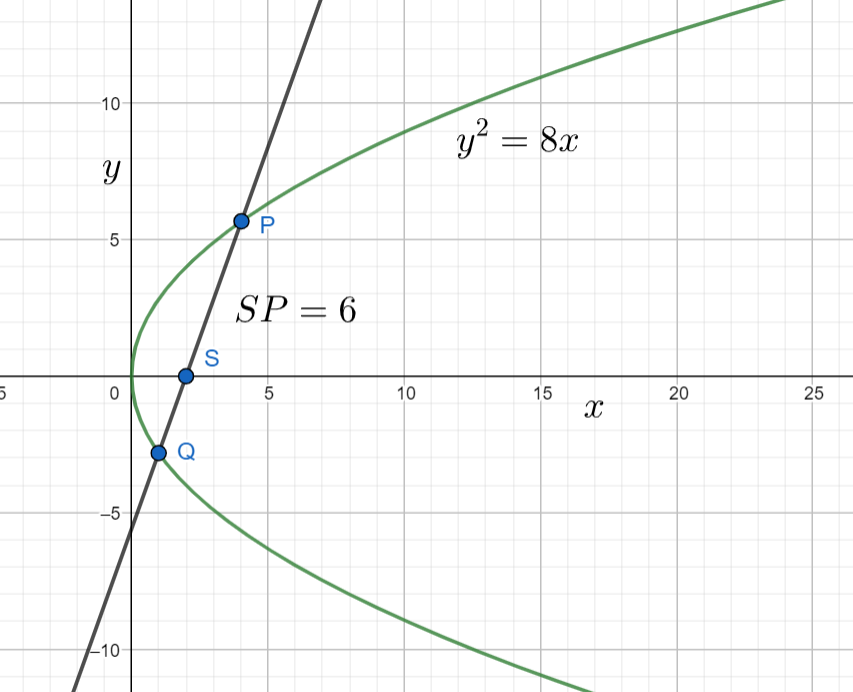
The value of semi latus rectum of the given parabola ${{y}^{2}}=8x$ is
$\begin{align}
  & \Rightarrow 2a=2\left( 2 \right) \\
 & \Rightarrow 2a=4 \\
\end{align}$
For a parabola the semi latus rectum of a parabola is the harmonic mean between the segments of any focal chord of a parabola.
Mathematically we can write $SP$, $4$, $SQ$ are in Harmonic Progression(H.P). So, we can write
$\Rightarrow \dfrac{2}{4}=\dfrac{1}{SP}+\dfrac{1}{SQ}$
Substituting the value of $SP=6$ in the above equation and simplifying the above equation, then we will get
$\begin{align}
  & \Rightarrow \dfrac{1}{2}=\dfrac{1}{6}+\dfrac{1}{SQ} \\
 & \Rightarrow \dfrac{1}{SQ}=\dfrac{1}{2}-\dfrac{1}{6} \\
 & \Rightarrow \dfrac{1}{SQ}=\dfrac{3-1}{6} \\
 & \Rightarrow \dfrac{1}{SQ}=\dfrac{1}{3} \\
\end{align}$
From the above equation we can write the value of $SQ$ as $SQ=3$.
Now the value of $\dfrac{SP}{SQ}$ will be
$\begin{align}
  & \Rightarrow \dfrac{SP}{SQ}=\dfrac{6}{3} \\
 & \Rightarrow \dfrac{SP}{SQ}=2 \\
\end{align}$

Note: For calculating the value of $SQ$ we can also another formula in H.P which is
$\Rightarrow 4=2\times \left( \dfrac{SP.SQ}{SP+SQ} \right)$
Substituting the value of $SP=6$ in the above equation, then we will get
$\begin{align}
  & \Rightarrow \dfrac{4}{2}=\dfrac{6.SQ}{6+SQ} \\
 & \Rightarrow 2\left( 6+SQ \right)=6SQ \\
 & \Rightarrow 6+SQ=3SQ \\
 & \Rightarrow SQ=3 \\
\end{align}$
From both the methods we got the value of $SQ$ as $SQ=3$.